Basiswissen

Ortslinien in der Geometrie

• Die Ortslinie wird oft auch Ortskurve genannt.
  

• In der Geometrie sind das Punkte mit gleichen Eigenschaften.
  

• Typische Ortslinien sind etwa Kreise, Geraden oder Parabeln.
  

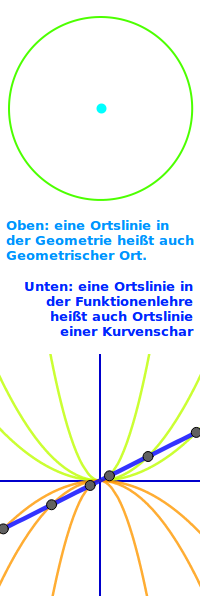
• Das klassische Beispiel ist der Kreis als Ortslinie ↗
  

Ortslinien einer Kurvenschar

• Die Ortslinie wird oft auch Ortskurve genannt.
  

• Bei Kurvenscharen interessiert oft, wo z. B. alle Hochpunkte liegen.
  

• Jeder Einzelkurve einer Schar kann ja einen eigenen Hochpunkt haben.
  

• Die Linie auf der alle Hochpunkte einer Schar lägen, wäre eine Ortslinie.
  

• Allgemein sprechen wir hier von der Ortslinie einer Kurvenschar ↗
  

Ortslinien als spezieller geometrischer Ort

• Bei einer Ortslinie bilden die Punkte eine zusammenhängende Linie.
  

• Man kann den Gedanken verallgemeinern:
  

• a) wenn die Punkte nicht zusammenhängen müssen,
  

• b) die Punkte auch Fächen oder Räume ergeben dürfen,
  

• dann ist die Punktemenge ein geometrischer Ort ↗
  

Fußnoten

• [1] Einer Gleichung F(x,y)=0 für die Koordinaten x und y entspricht oft eine Kurve, die die Eigenschaft hat, dass die Koordinaten jedes beliebigen Kurvenpunktes P der Gleichung genügen und dass umgekehrt jeder Punkt, dessen Koordinaten diese Gleichung erfüllen, auf der Kurve liegt. Die Menge dieser Punkte wird auch geometrischer Ort genannt." In: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Dort die Seite 200.
  

• [2] "Kreis, geometrischer Ort aller Punkte in der Ebene, die von einem Punkt M dieser Ebene die gleiche Entfernung r haben." In: Guido Walz: Spektrum Lexikon der Mathematik. Band 3: Imp bis Mon; 2002; ISBN: 3-8274-0435-5. Dort der Artikel "Kreis". Siehe auch Kreis als geometrischer Ort ↗
  

• [3] Ortslinie als Sonderfall des geometrischen Orts: Wikipedia Artikel "Geometrischer Ort". 6. Juni 2021: "In der Elementargeometrie bezeichnet geometrischer Ort (Plural: geometrische Örter) eine Menge von Punkten, die eine bestimmte, gegebene Eigenschaft haben. In der ebenen Geometrie ist dies in der Regel eine Kurve, wofür man auch das Wort Ortskurve oder Ortslinie verwendet."