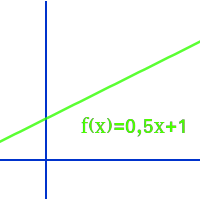
Graph aus Gleichung
Begriffsklärung | Beispiele
© 2016
- 2025
Basiswissen|
Was meint Graph?|
Was meint Gleichung hier?|
Wie zeichnet man den Graphen?|
Gibt es einfachere Methoden?|
Geometrischer Ort
Basiswissen
Auf dieser Seite wird erklärt, wie man durch Einsetzen von x-Werten schnell eine Idee vom ungefähren Verlauf eines Funktionsgraphen erhält. Vorgestellt wird auch die Idee von einem geometrischen Ort.
Was meint Graph?
- Graph meint hier Punkte in einem x-y-Koordinatensystem.
- Solche Graphen nennt man auch Funktionsgraphen.
- Die Punkte können eine Linie oder Kurve geben.
- Die Punkte können auch eine Fläche oder sonstwas geben.
- Alle Punkte im Koordindatensystem würde man Graph nennen.
- Siehe auch 👉 Funktionsgraph
Was meint Gleichung hier?
- Das meint eine Gleichung mit mindestens einer Unbekannten.
- Die Gleichung kann auch mehrere Unbekannte haben.
- Zu jeder Gleichung kann man einen Graphen zeichnen.
- Siehe allgemein dazu unter 👉 Graph zeichnen
Wie zeichnet man den Graphen?
- Dazu gibt es sehr viele verschiedene Verfahren.
- Betrachten wir das Beispiel: y = 0,5x²+2
- Was immer geht: für x irgendwelche Werte einsetzen (möglichst einfache), dazugehörigen y-Wert ausrechnen.
- Zum Beispiel: x=2 gehört zu y=4
- Zum Beispiel: x=1 gehört zu y=2,5
- Zum Beispiel: x=0 gehört zu y=2
- Und so weiter mit möglichst vielen Zahlen.
- Diese Wertepaare werden oft auch als Tabelle dargestellt.
- Jedes Wertepaar kann man als Punkt in ein Koordinatensystem eintragen.
- Man macht das dann für viele x-Werte und so entsteht nach und nach ein Graph.
- Diese Methode geht immer, kann aber sehr aufwändig sein.
- Mehr dazu unter 👉 Graph aus Tabelle
Gibt es einfachere Methoden?
- Ja, und zwar je nach Funktionsart:
- Sehr einfach ist es bei Geraden 👉 Graph aus Geradengleichung
- Etwas schwerer ist es bei Parabeln 👉 Graph aus Parabelgleichung
- Bei anderen Funktionen, lies unter 👉 Graph über Kurvendiskussion
Geometrischer Ort
- Betrachtet man die Lösung von Gleichungen vor allem geometrisch ...
- so spricht man auch von einem geometrischen Ort.
- Der Ort sind alle Punkte, die für eine Lösung der Gleichung stehen.
- Geometrische Örter können Punkte, Linien, Parabeln, Kreise oder auch Kugeln und Quader sein.
- Mehr dazu unter 👉 Geometrischer Ort