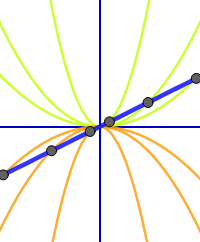
Ortslinie einer Kurvenschar berechnen

7 Einsteigeraufgaben für die Oberstufe

Scheitelpunkte von Parabelscharen

a) ft(x) = -2x² + tx - 1

Bildbeschreibung und Urheberrecht — Mehrere Parabeln bilden zusammen die Schar fa(x)=ax². Für jede Parabel wurde der Punkt mit der Steigung 1 bestimmt. Die Punkte ergeben miteinander die blaue Gerade. Das ist die Ortslinie zu allen Punkten mit der Steigung 1 für diese Schar.☛

c) ft(x) = x² + tx - t

Hochpunkte einer kubischen
(hoch drei) Funktionsschar

d) fk(x) = -2x³ + kx

Wendestellen einer quartischen
(hoch vier) Funktionsschar

e) fk(x) = x^4 - kx^2

Wendestellen einer Schar
von Exponentialfunktionen

f) fk(x) = (e^x - k)^2

Wendepunkte einer Schar
von Logarithmusfunktionen

g) fk(x) = x + ln(x² + k) für natürliche k

Lösungen

a) o(x) = 2xx-1
b) o(x) = 0,5x
c) o(x) = -xx + 2x
d) o(x) = 4x^3
e) o(x) = -x^4

f) o(x) = e^(2x)
g) o(x) = x + ln(2xx)