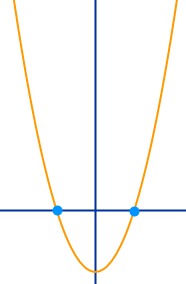
Nullstellen von reinquadratischen Funktionen bestimmen
Übersicht
© 2017
- 2025
Basiswissen|
Bauplan|
Legende|
c interpretieren|
pq-Formel|
Symmetrie|
Umformen|
Faktorisieren|
ABC-Formel|
Tipps|
Aufgaben dazu
Basiswissen
f(x) = ax² + c ist der Bauplan einer reinquadratischen Funktion. Es gibt immer ein Glied mit x². Es darf noch ein Glied ohne x geben, das sogenannte absolute Glied. Was nicht vorkommen darf sind sogenannte lineare Glieder, also ein Glied mit x ohne hoch zwei. Solche Gleichungen lassen sich immer leicht über Umformen lösen. Da ist hier erklärt.
Bauplan
- f(x) = ax² + c
Legende
f(x) = Funktionswert, wird oft auch y genannt.
x² = meint x mal x, ausgesprochen x-quadrat.
a = eine beliebige (außer Null) konstante Zahl, die aber fest vorgegeben ist
c = eine beliebige (Null erlaubt) konstante Zahl, die aber fest vorgegeben ist
c interpretieren
- Wenn das absolute Glied c gleich 0 ist, dann ist x=0 die einzige NS.
- Wenn das absolute Glied c addiert wird, dann gibt es gar keine NS.
- Wenn das absolute Glied c abgezogen wird, dann gibt es zwei NS.
- Im letzten Fall muss man sie dann mit einem der Verfahren unten bestimmen.
pq-Formel
- Die pq-Formel funktioniert für reinquadratische Funktionen immer.
- Immer erst f(x) gleich Null setzen.
- Wenn a ungleich 1 ist, erst beide Seiten durch a teilen.
- Wenn a gleich 1 ist (also nur x² dasteht), direkt weitgergehen.
- Jetzt steht links vom Gleichheitszeichen die Zahl 0.
- Rechts vom Gleichheitszeichen steht x² + c/a
- p ist bei reinquadratischen Funktionen immer 0!
- q ist bei reinquadratischen Funktionen immer das c/a.
- Damit die pq-Formel rechnen, gibt immer die NS.
Symmetrie
- Der Graph reinquadratischer Funktionen ist immer achsensymmetrisch zur y-Achse.
- Wenn es also zwei Nullstellen gibt, sind sie immer Gegenzahlen zueinander.
- Beispiel: wenn 4 eine NS ist, dann ist automatisch auch -4 eine NS.
Umformen
- Geht bei reinquadratischen Funktionen immer.
- Immer erst f(x) gleich Null setzen.
- Links vom Gleichheitszeichen steht dann 0.
- Jetzt nach x umstellen:
- Wenn am Ende "-c" steht, schreibe es als +(-c).
- Jetzt auf beiden Seiten c abziehen.
- Dann beide Seiten durch a teilen.
- Dann von beiden Seiten die Wurzel ziehen.
- Zwei Lösungen hinschreiben:
- Einmal die ausgerechnete Wurzel ...
- und einmal die ausgerechnete Wurzel mit einem Minus davor.
Faktorisieren
- Geht nur, wenn absolutes Glied negativ ist.
- Immer erst f(x) gleich Null setzen.
- Beispiel: 0=ax²-c ⭢ geht
- Beispiel: 0=ax²+c ⭢ geht nicht
- Falls a ungleich 1 ist, erst beide Seiten durch a teilen.
- Dann faktorisieren über dritte binomische Formel rückwärts.
- Gibt: 0 = (x+c/a)(x-c/a)
- Ablesen über den 👉 Satz vom Nullprodukt
- NS bei -c/a und bei +c/a
ABC-Formel
- Geht immer, ist aber bei reinquadr. Funktionen unnötig aufwändig
- Das A aus der Formel wäre das a aus der Funktionsgleichung oben.
- Das B aus der Formel wäre immer die Null (da kein Term mit x).
- Das C aus der Formel wäre immer das c aus der Funktionsgleichung.
- Damit jetzt die ABC-Formel rechnen
- Siehe auch 👉 ABC-Formel
Tipps
- 1/2 mal 1/2 gibt ein 1/4.
- 1/3 mal 1/3 gibt ein 1/9.
- 0.25 ist wie ein 1/4.
Aufgaben dazu
Zu diese Aufgabentyp gibt es Übungen mit Lösungen als Quickchecks. Direkt zu den Aufgaben geht es über => qck