Nullstellen von reinquadratischen Funktionen über Faktorisieren
3. binomische Formel rückwärts
© 2017
- 2025
Basiswissen
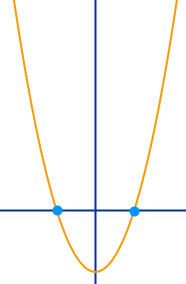
0 = 4x²-36 kann mit Hilfe der dritten binomischen Formel gelöst werden. Dieser Weg ist schneller als die Anwendung der pq-Formel (ginge auch). Das ist hier kurz mit einem Beispiel und mit Übungsaufgaben dazu vorgestellt.
Vorbereitung
- Bringe die Funktionsgleichung auf die Form: f(x) = ax² + c
- Setze f(x) zuerst immer gleich 0. Das gibt: 0 = ax² + c
- Falls c positiv ist, dann gibt es keine NS (fertig)
- Falls c gleich 0 ist, dann ist x=0 die einzige NS (fertig)
- Falls c negativ ist, dann gehe die folgenden Schritte durch.
3. binomische Formel
- Beispiel: 0 = 4x² - 36
- Beide Seiten durch a teilen, gibt hier: 0 = x² - 9.
- Absolutes Glied c als Quadrat schreiben: 0 = x² - 3²
- An 3. binomische Formel erinnern: (a+b)(a-b) = a² - b²
- Diese Formel wird jetzt rückwärts genutzt, gibt hier:
- 0 = (x+3)(x-3)
Satz vom Nullprodukt
- Nun nutzt man den 👉 Satz vom Nullprodukt
- Lies darüber die Nullstellen einfach ab:
- Gibt hier: Nullstellen bei -3 und 3 ✔