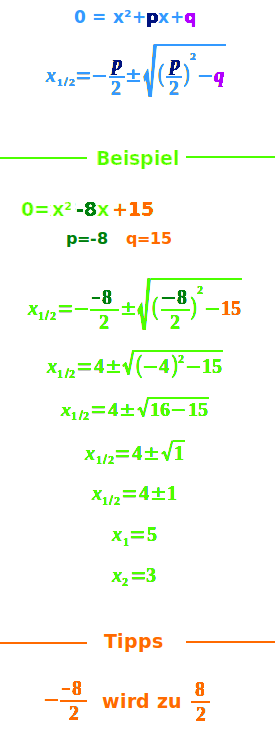pq-Formel

Übersicht

Basiswissen｜ Der Nutzen der Formel｜ Formel｜ Wann kann man die pq-Formel nutzen?｜ 1. Schritt: Normalform prüfen｜ 2. Schritt: Normalform herstellen｜ 3. Schritt p und q festlegen｜ Tipp｜ Sonderfall: das p fehlt｜ Sonderfall: das q fehlt｜ 4. Schritt: p und q in Formel einsetzen｜ Tipp: wie viele Lösungen es geben kann｜ Beispiel I｜ Beispiel II｜ Beispiel III｜ Aufgaben dazu

Basiswissen

p/2 ± √((p/2)²-q) ist die Standardformel zum Lösen einer quadratischen Gleichung. Die Gleichung muss dabei in der sogenannten Normalform gegeben sein: 0 = x² + px + q. Das ist näher erklärt.

Bildbeschreibung und Urheberrecht — Die pq-Formel: vor allem die sichere Handhabung der Vorzeichen benötigt viel Aufmerksamkeit.☛

Der Nutzen der Formel

Mit der pq-Formel kann man immer alle Lösungen einer quadratischen Gleichung finden. Man kann mit dieser Formel aber auch nur die Lösungen von quadratischen Gleichungen finden. Hier stehen einige typische quadratische Gleichungen:

x²-8x+15 = 0

4x-20x+24 = 0

x²+10x = -24

x² + 4x = 0

x² = 729

Jede dieser Gleichungen kann man mit der pq-Formel lösen. Oft gibt es auch noch andere Lösungsmethode. Manchmal, je nachdem wie die Gleichung mit ihren Zahlen aussieht, kann eine andere Lösung auch deutlich schneller sein. Der große Vorteil der pq-Formel ist aber, dass sie immer mit demselben Schema durchgeführt werden kann. Das gilt für die anderen Lösungswege meist nicht. Die pq-Formel ist also dann ideal, wenn man zunächst nur einen Lösungsweg für alle Aufgaben lernen möchte.

Formel

x = -p/2 ± Wurzel aus [(p/2)²-q]

x = -p/2 ± √[(p/2)²-q]

Wann kann man die pq-Formel nutzen?

Die pq-Formel gilt nur für eine 👉 quadratische Gleichung

Mit der pq-Formel kann man jede quadratische Gleichung lösen.

Man braucht immer die 👉 Normalform der quadratischen Gleichung

Das wird hier jetzt näher erklärt.

MERKSATZ:

1.0: Die pq-Formel kann man immer zum Lösen von quadratischen Gleichungen benutzen. Man kann sie aber auch nur zum Lösen von quadratischen Gleichungen nutzen. ✓

1. Schritt: Normalform prüfen

Um die pq-Formel anwenden zu können, muss die gegebene quadratische Gleichung in der sogenannten Normalform vorliegen. Steht die Gleichung noch nicht in dieser Normalform, muss man sie erst dazu umformen. Hier ist erst erklärt, wie diese Normalform aussieht:

0 = x² + px + q

Links vom Gleichzeichen darf nur 0 stehen.

Rechts kommt zuerst das x² ohne irgendetwas davor.

Dann darf ein + oder - mit einer Zahl und einem x danach kommen.

Am Ende darf ein + oder - mit einer Zahl ohne x kommen.

Normalform nicht OK: 4=x²-8x+16 | links keine 0

Normalform nicht OK: 0=2x²-8x+16 | 2 vor dem x²

Normalform nicht OK: 0=-x²-8x+16 | - vor dem x²

Normalform OK: 0=x²-8x+16 ✔

Normalform OK: 0=x²+4x+0 ✔

Normalform OK: 0=x²+0x+4 ✔

Normalform OK: 0=x²+0x+0 ✔

MERKSATZ:

2.0: Die pq-Formel kann man nur verwenden, wenn man die quadratische Gleichung in der Normalform 0 = x²+px+q gegeben hat. Vor dem x² darf nichts mehr stehen. ✓

2. Schritt: Normalform herstellen

Ist die quadratische Gleichung noch nicht in der Normalform gegeben, muss man sie erst umformen. Hier sind kurz einige der häufigsten Fälle beschrieben.

Ziel

x² + px + q = 0

Methoden

0 = x²-7x+21 -> 0 auf der falschen Seite -> Seiten tauschen -> x²-7x+21 = 0 ✓

-16x+x²+63 = 0 -> falsche Reihenfolge -> umsortieren -> x²-16x+63 = 0 ✓

-x²+20x-24 = 0 -> Minuszeichen vor dem x² -> mal -1 -> x²-20x+24 = 0 ✓

4x²-20x+24 = 0 -> 4 vor x² -> durch 4 teilen -> x²-5x+6 = 0 ✓

x²-16 = 0 -> p fehlt -> heißt: p=0 -> x²+0x-16 = 0 ✓

x²+4x = 0 -> q fehlt -> heißt: q=0 -> x²+4x+0 = 0 ✓

Das waren nur einige wenige Beispiele. Eine ausführliche Erklärung, wie man eine quadratische Gleichung in die Normalform umwandelt steht im Artikel 👉 Normalform für pq-Formel herstellen

3. Schritt p und q festlegen

Man hat die Normalform: 0 = x² - 8x + 15

p und q aus der Normalform ablesen:

Das p ist der Faktor (Zahl) vor dem x.

Achtung: das Vorzeichen gehört dazu.

Im Beispiel ist das p die Zahl -8.

Das q ist die alleinstehende Zahl ohne x.

Im Beispiel ist das p die +15

MERKSATZ:

3.0: Die Vorzeichen gehören zum p und zum q. Bei 0 = x²-8x+15 ist p=-8 und q=8. ✓

Tipp

Ein Vorzeichen gehört immer mit zur Zahl.

Wenn vor dem x keine Zahl steht, dann ist p=1.

Sonderfall: das p fehlt

Wenn es gar kein x ohne Quadrat gibt, dann ist p=0.

Beispiel: 0 = x² + 16 ⭢ p = 0

Sonderfall: das q fehlt

Wenn es am Ende keine Zahl für q gibt, dann ist q=0.

Beispiele: 0 = x² - 4x ⭢ q = 0

MERKSATZ:

4.0: Fehlt das Glied nur mit, so ist p=0. Fehlt das Glied ganz ohne x (nur Zahl), dann ist q=0. ✓

4. Schritt: p und q in Formel einsetzen

Setze die Zahlen von oben für p und q ein:

Erste Nullstelle: x₁ = -p/2 + Wurzel aus [(p/2)² - q]

Zweite Nullstelle: x₂ = -p/2 - Wurzel aus [(p/2)² - q]

Tipp: wie viele Lösungen es geben kann

Der Term unter der Wurzel heißt Diskriminante.

Ist die Diskriminante kleiner als Null, dann gibt es keine Lösungen.

Ist die Diskriminante genau gleich Null, dann gibt es genau eine Lösung.

ist die Diskriminante größer als Null, dann gibt es zwei Lösungen.

Mehr unter 👉 Diskriminante bei pq-Formel

Beispiel I

0 = x² -8x + 15
p = -8
q = 15
x₁ = 5 ✔
x₂ = 3 ✔

Beispiel II

0 = x² + 4x
p = 4
q = 0
x₁ = -4 ✔
x₂ = 0 ✔

Beispiel III

0 = x² - 16
p = 0
q = -16
x₁ = -4 ✔
x₂ = 4 ✔

Aufgaben dazu

Aufgaben zur pq-Formel sind hier als Quickcheck zusammengestellt. Zu jeder Aufgabe gibt es immer auch eine Lösung. Direkt zu den Aufgaben geht es über => qck