Diskriminante bei pq-Formel
… (p/2)²-q
Basiswissen
Die pq-Formel lautet: x = -p/2 ± √[(p/2)²-q]. Der Term [(p/2)²-q] steht unter der Wurzel und heißt Diskriminante. Ober er kleiner als 0, genau 0 oder größer als 0 ist gibt an, wie viele Lösungen eine quadratische Gleichung hat.
Was ist die Diskriminante?
- x = -p/2 ± √[(p/2)²-q]
- Bei der pq-Formel kommt rechts eine Wurzel vor.
- Die Diskriminante ist das, was unter dem Wurzelzeichen steht.
- Die Diskriminante ist also der Term: (p/2)²-q
- Eine häufige Abkürzung ist ein großes D.
Wie berechnet man D?
- Die pq-Formel gibt Lösungen für quadratische Gleichungen.
- Wenn man das p und das q von einer Gleichung eingesetzt hat, ...
- dann kann man den Zahlenwert ausrechnen, der unter der Wurzel steht.
- Bei der pq-Formel heißt dieser Zahlenwert Diskriminante.
- Man kürzt sie oft ab mit D.
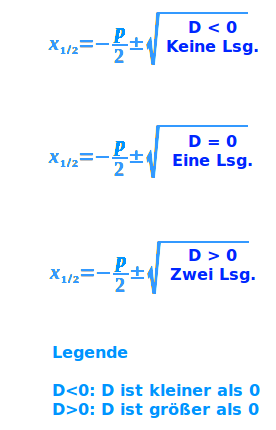
Was sagt D?
- Ist die D kleiner als Null, dann hat die Gleichung keine Lösungen.
- ist die D genau gleich Null, dann hat die Gleichung genau eine Lösung.
- Ist die Di größer als Null, dann hat die Gleichung zwei Lösungen.
Beispiel I
- Man hat die Gleichung 0 = x² - 6x + 10
- p wäre hier -6 und q wäre 10.
- In der pq-Formel gibt das unter der Wurzel: 9-10=-1
- D ist negativ, also hat die Gleichung Lösungen.
- Man schreibt: die Gleichung ist nicht lösbar.
- Siehe auch 0=x²+4x+8 ↗
Beispiel II
- Man hat die Gleichung 0 = x² -6x + 9
- p wäre hier -6 und q wäre 9.
- In der pq-Formel gibt das unter der Wurzel: 9-9=0.
- D ist genau 0, es gibt also genau eine Lösung.
- (Nämlich nur die Zahl 3)
Beispiel III
- Man hat die Gleichung 0 = x² -6x + 8
- p wäre hier -6 und q wäre 8.
- In der pq-Formel gibt das unter der Wurzel= 9-8=1.
- D ist größer als Null, es gibt also zwei Lösungen.
- (Nämlich 8 und 10)
Woher kommt das Wort?
- Discriminare ist Latein.
- Es heißt: trennen, scheiden, unterscheiden.
Tipps
- Kleiner als Null schreibt man oft: D < 0
- Größer als Null schreibt man auch: D > 0
