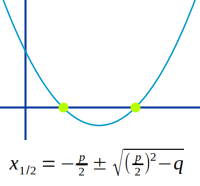
Nullstellen über pq-Formel
-p/2 ± √[(p/2)²-q]
© 2016
- 2025
Basiswissen|
Was sind NS von Parabeln?|
Wann funktioniert die pq-Formel?|
Was muss gegeben sein?|
0 setzen|
p und q ablesen|
Einsetzen|
Tipps|
Beispiel I|
Beispiel II|
Beispiel III
Basiswissen
f(x) = x²-6x+8 ist eine quadratische Funktion. Das p ist hier die Zahl -6 und q ist 8. In die Formel eingesetzt erhält man die x-Werte, bei denen die Parabel die x-Achse schneidet, also die Nullstellen. Im Beispiel sind es x=2 und x=4. Das Lösungsverfahren wird hier Schritt-für-Schritt erklärt.
Was sind NS von Parabeln?
- Der Graph einer quadratischen Funktionen heißt Parabel.
- Die x-Achse ist die Achse von links nach rechts (waagrecht).
- Eine Nullstelle ist der x-Wert, wo ein Graph die x-Achse schneidet.
- Statt Nullstelle sagt man auch x-Achsenabschnitt.
- Mit der pq-Formel findet man diese Stellen.
Wann funktioniert die pq-Formel?
- Die pq-Formel funktioniert nur für quadratische Funktionen.
- Die pq-Formel funktioniert für jede quadratische Funktion.
Was muss gegeben sein?
- Die Funktionsgleichung muss in Normalform gegeben sein.
- Die Normalform lautet f(x) = x² + px + q
- Statt dem f(x) darf links auch y stehen.
- Mehr unter 👉 Normalform für pq-Formel
0 setzen
- Man setzt f(x) immer erst 0.
- Wo vorher ein f(x) stand, schreibt man also eine 0 hin.
- Dasselbe gilt für ein y: man würde dort eine 0 hinschreiben.
- Man hat jetzt eine Gleichung der Form: 0 = x² + px + q
p und q ablesen
- Für die Formel braucht man Zahlen für p und q.
- Das p ist der Faktor vor dem x (das x ohne ²).
- Das q ist die alleinstehende Zahl ohne x.
- Die Vorzeichen gehören immer mit zur Zahl.
Einsetzen
- Die pq-Formel rechnet man einmal mit + und einmal mit -.
- Als Ergebnis können zwei verschiedene Zahlen rauskommen.
- Die Zahlen für p und q setzt man in die Formel ein:
- 1. Nullstelle: -p/2 + Wurzel aus [(p/2)² - q]
- 2. Nullstelle: -p/2 - Wurzel aus [(p/2)² - q]
Tipps
- Was unter der Wurzel steht heißt Radikand.
- Wenn der Radikand negativ ist, gibt es keine NS.
- Wenn p negativ ist steht ganz am Anfang minusminus.
- Das Minusminus am Anfang wird dann zu einem Plus.
- Wenn das q negativ ist, steht unter der Wurzel minusminus.
- Dieses Minusminus wird dann zu einem Plus.
Beispiel I
- x² + 4x
- p=4 und q=0
- NS (0|0) und (-4|0)
Beispiel II
- x² - 16
- p=0 und q=-16
- NS (-4|0) und (4|0)
Beispiel III
- x² + 2x + 24
- p=2 und q=24
- Keine NS.