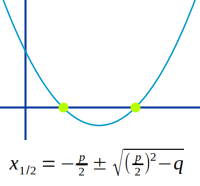
Nullstellen über pq-Formel
20 Aufgaben und Verständnisfragen
© 2016
- 2026
Basiswissen|
Was sind NS von Parabeln?|
Wann funktioniert die pq-Formel?|
Was muss gegeben sein?|
0 setzen|
p und q ablesen|
Einsetzen|
Tipps|
Beispiel I|
Beispiel II|
Beispiel III
Grundidee
Mit der pq-Formel kann man von jeder quadratischen Gleichung immer alle Nullstellen finden. Gib alle Nullestellen der Gleichungen an. Hat eine Gleichung keine Nullestellen (kann, muss aber hier nicht vorkommen), dann schreibe "keine NS". Mache immer die Probe.
Aufgaben
a) 0 = x² - 10x + 24
b) 0 = x² + 5x - 50
c) 0 = x² - 300x + 20000
d) 0 = x² + 110x + 1000
e) 0 = x² - 0,75x + 0,125
f) 0 = x² - 0,6x + 0,05
g) 0 = x² - 21x + 110
h) 0 = x² - 10000
i) 0 = x² + 10000
j) 0 = x²
k) 0 = 2x² - 20x + 48
l) 0 = 0.1x² + 0.5x - 5
m) 0 = 3x² - 900x + 60000
n) 0 = 0.1x² + 11x + 100
o) 0 = 4x² - 3x + 0,5
Wahr oder falsch?
p) Die pq-Formel liefert nicht automatisch alle NS einer Funktion.
q) Manchmal liefert die pq-Formel NS, die es gar nicht wirklich gibt.
r) Wenn es NS gibt, dann kann man sie immer über die pq-Formel finden.
s) Wenn das p=0 ist, dann kann es niemals eine Nullstelle geben.
t) Wenn das q=0 ist, dann kann es niemals eine Nullstelle geben.
Lösungen
a) 6 und 4
b) -10 und 5
c) 200 und 100
d) -100 und -10
e) 0,5 und 0,25
f) 0,5 und 0,1
g) 10 und 11
h) 100 und -100
i) Keine NS
j) Nur 0
k) 6 und 4
l) -10 und 5
m) 200 und 100
n) -100 und -10
o) 0,5 und 0,25
Wahr oder falsch?
p) falsch
q) falsch
r) wahr
s) falsch
t) falsch