Normalkraft
Physik
Definition
Das Wort Normalkraft wird meist im Zusammenhang mit einer schiefen Ebene betrachtet.[1] Als Normalkraft bezeichnet man eine Kraft, die senkrecht von einer Fläche weg auf ein Objekt auf der Fläche wirkt. Die Normalkraft ist eine Reaktionskraft die der Gewichtskraft entgegen wirkt. Senkrecht heißt hier: im 90°-Winkel. Hier steht die Formel zur Berechnung und ein Anwendungsfall.
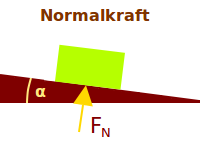
Entstehung und Wirkung der Normalkraft
Liegt ein Gegenstand auf einer Ebene und wirkt auf diesen Gegenstand eine Schwerkraft, zum Beispiel die Erdanziehungskraft, dann drückt dieser Gegenstand auf den Untergrund. Nach dem dritten Newtonschen Axiom wirkt der Untergrund dann mit einer Gegenkraft auf den Gegenstand zurück, sodass dieser nicht in den Untergrund eindringen kann. Dieser Kraft vom Untergrund hin zum Gegenstand ist die sogenannte Normalkraft. Die Normalkraft beeinflusst vor allem den Effekt einer Haft- und Rollreibung zwischen dem Gegenstand und seiner Auflagefläche. Je steiler die Fläche gestellt ist, desto geringer ist die Normalkraft. Am größten ist die Normalkraft bei einer waagrechten Fläche, am kleinsten (nämlich 0 Newton) ist sie bei einer senkrechten Fläche, etwa einer (Steil)Wand.
Berechnung der Normalkraft mit schiefer Ebene
F = m·g·cos(α) - dabei ist F die gesuchte Normalkraft, m die Masse des Objektes auf einer schiefen Ebene, g der Ortsfaktor, z. B. 9,81 N/kg, und α ist der Steigungs- oder Neigungswinkel alpha.
- F ist die Normalkraft [hier gesucht] ↗
- m ist die Masse [des Objektes auf der Ebene] ↗
- g ist der Ortsfaktor [oft 9,81 N/kg] ↗
- α ist der Neigungswinkel [der Ebene] ↗
- cos ist der Cosinus [Trigonometrie] ↗
Der Cosinus und die Normalkraft
Der Cosinus, auch Kosinus geschrieben, ist eine sogenannte trigonometrische Funktion. Kennt man den Neigungswinkel einer schiefen Ebene, dann gibt der Cosinus sozusagen den Anteil einer Kraft an der Gewichtskraft eines Objektes, der senkrecht zur Auflage wirkt. Um den passenden Cosinuswert zu einem Winkel zu bestimmen, benutzt man zum Beispiel eine Cosinustabelle Grad ↗
Rechenbeispiel zur Normalkraft
Angenommen man hat eine schiefe Ebene mit einer Hangneigung von etwa 20 Grad. Zum Vergleich: die steilste Straße der Welt ist die Baldwin Straße in Neuseeland mit 19,3° Neigung. Und angenommen man fährt auf dieser Straße mit einem Fahhrad bergauf oder bergab. Das Objekt im Sinne der Physik ist dann das Fahhrad mit dem Fahrer zusammen. Nehmen wir die Gesamtmasse mit 100 kg an. Dann kann man die Normalraft F berechnen über F = 100 kg · 9,81 N/kg · cos(20°). Das Ergebnis ist ungefähr 922 Newton.
Die Normalkraft und der Rollwiderstand
Fährt man mit einem Fahrrad über eine feste ebene Betonfläche muss man sehr viel weniger stark treten wie bei einer Fahrt mit derselben Geschwindigkeit über eine ebenfalls ebene Gummimatte oder - noch sehr viel extremer - über eine ebene sandige Fläche. Interessant ist auch die Beobachtung, dass man mit prall gefüllten Fahrradreifen sehr viel weniger Kraft und Energie nötig hat als mit schwach aufgepumpten Reifen. Um Energie und Kraft zu sparen, möchte man den Rollwiderstand oft möglichst klein halten. Fährt man auf einer schiefen Ebene, geht der Rollwiderstand deutlich zurück, je steiler die Ebene, desto weniger Rollwiderstand. Wesentlich für den Einfluss der Steilheit der Fahrfläche ist die sogennante Normalkraft [in Newton] ↗
Die Normalkraft und die Haftreibung
Die Haftreibung ist ein anderer Effekt und hat andere Ursache als die Rollreibung (Rollwiderstand): liegt ein Gegenstand sicher ohne zu Rutschen auf einer schiefen Ebene, ist die Her Haftreibung zwischen dem Gegenstand und der Ebene ausreichend groß, um den Gegenstand fest zu halten. Die Normalkraft drückt ihn sozusagen auf die Fläche und hält ihn daran fest. Stellt man die Fläche nun immer steiler, wird der Gegenstand irgendwann ins Rutschen kommen. Mit der Steilheit geht die Normalkraft zurück, irgendwann genügt sie nicht mehr, um den Gegenstand ausreichend stark an die Fläche zu drücken. Siehe auch Haftreibung ↗
Ein Extremfall: Steilwandfahrer
Auf Jahrmärkten stellen sogenannte Steilwandfahrer ihre Kunst zur Schau: mit einem Motorrad fahren die Artisten an einer senkrechten Fläche im Kreis. Wieder ist die Normalkraft die Kraft, die von der Fläche (Steilwand) auf das Objekt (Motorrad mit Fahrer) wirkt. Ursache der Normalkraft ist jetzt allerdings nicht die Schwerkraft, deren Anteil bei einer senkrechten Fläche ja Null Newton ist. Ursache der Normalkraft ist jetzt die Zentrifugalkraft des ausreichend schnellen Motorradfahrers. Diese Zentrifugalkraft wirkt nach außen, die Steilwand wirkt mit einer Gegenkraft, der Zentripetalkraft nach innen hin zurück. Diese Zentripetalkraft ist auch die Normalkraft. Siehe auch Steilwand (Jahrmarkt) ↗
Veraltete Bedeutung
Bis mindestens in Jahr 1908 bezeichnet man auch Radialkräfte einer Kreisbewegung als Normalkraft, speziell die Zentripetalkraft.[2][3] Diese Deutung ist heute nicht mehr üblich. Man spricht von einer Zentripetalkraft ↗
Fußnoten
- [1] Normalkraft auf einer schiefen Ebene: "Wird das Gewicht P eines auf die s. E. gelegten Körpers durch die vertikale Linie ba dargestellt, so kann man sich diese Kraft nach dem Satz vom Parallelogramm der Kräfte in zwei Seitenkräfte zerlegt denken, deren eine bc (die Parallelkraft, Q) parallel zur schiefen Ebene wirkt und das Herabgleiten des Körpers längs derselben verursacht, während die andre bd (die Normalkraft, R), senkrecht zur schiefen Ebene gerichtet, durch deren Widerstand aufgehoben wird und, falls keine Reibung stattfindet, zur Bewegung nichts beiträgt." In einer Skizze zeigt die Normalkraft bd von einem aufliegenden Körper hin auf die Oberfläche der schiefen Ebene. Die Normalkraft ist damit die senkrecht auf die Ebene wirkende Komponente der Gewichtskraft. Nach heutiger (2024) Sicht ist die Normalkraft jedoch eine Reaktionskraft der Ebene auf den auf ihr liegenden Körper. Damit zeigt die Normalkraft der heutigen Deutung in die entgegengesetzte Richtung wie in der Definition aus dem Jahr 1909. In: Meyers Großes Konversations-Lexikon, Band 17. Leipzig 1909, S. 754-755. Online: http://www.zeno.org/nid/20007418949
- [2] Heute veraltet ist die Bedeutung der Normalkraft als Zentripetalkraft: "Normalkraft, so v.w. Centripetalkraft." In: Pierer's Universal-Lexikon, Band 12. Altenburg 1861, S. 109. Online: http://www.zeno.org/nid/20010526978
- [3] Heute veraltet ist die Bedeutung der Normalkraft als Zentripetalkraft: "Normalkraft (Normalkomponente). Die bewegende Kraft m φ eines Punktes von der Masse m, welche ihm die Beschleunigung φ zu erteilen vermag, kann in zwei Komponenten gespalten werden, die Tangentialkraft m φt = m dv/dt und die Normalkraft m φn = m v2/ρ. Erstere wirkt in der Richtung der Tangente der Bahn und verändert die Geschwindigkeit nach Größe allein; letztere ändert die Richtung der Geschwindigkeit ab, sie bewirkt die Krümmung der Bahn und ist nach dem Krümmungsmittelpunkte derselben gerichtet. Beide gehen aus der Tangential- und Normalbeschleunigung φt und φn durch Multiplikation mit der Masse m hervor. S. Beschleunigung, Bd. 1, S. 717." In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 6 Stuttgart, Leipzig 1908., S. 662-663. Online: http://www.zeno.org/nid/20006093795
