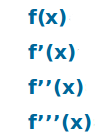Basiswissen

f'(x), f''(x) oder auch f'''(x): die Lagrange-Notation ist eine von mehreren Schreibweisen für Ableitungen. Hier stehen die drei ersten Ableitungen kurz aufgelistet.

Bildbeschreibung und Urheberrecht — Die Schreibweise mit gestrichenem f nennt man die Lagrange-Notation. Sie ist gedanklich eng verbunden mit dem Wort Analysis.☛

f(x) = x³ ⭢ f'(x) = 3x² 👉 erste Ableitung

f(x) = x³ ⭢ f''(x) 6x¹ 👉 zweite Ableitung

f(x) = x³ ⭢ f'''(x) 6 👉 dritte Ableitung

Gibt es auch noch höhere Ableitungen?

Ja, theoretische kann man jede Ableitung wieder ableiten. Ist die Ableitung einer Funktion irgendwann einmal 0, so gibt es aber bei höheren Ableitungen dann keine weitere Veränderungen mehr. Egal wie oft man weiter ableitet, es wird immer wieder 0 herauskommen. Eine Formel in der theoretisch unendlich hohe Ableitungen vorkommen ist die sogenannte 👉 Taylor-Reihe

Welche anderen Schreibweisen gibt es?

f', f'', f''' etc. heißt 👉 Lagrange-Notation

dy/dx, d²y/dx², d³y/dx³ etc. heißt 👉 Leibniz-Notation

x mit einem oder mehreren Punkten ist die 👉 Newton-Notation

Siehe auch 👉 Notationen von Ableitungen