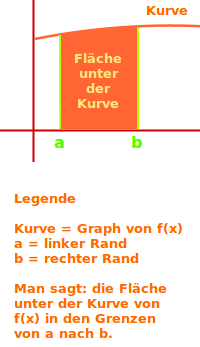
Fläche unter der Kurve berechnen
Anleitungen
Basiswissen
Die Fläche unter der Kurve meint immer eine Flächen, die von einem Funktionsgraphen, der x-Achse und eventuell noch von zwei senkrechten Strecken umrandet wird. Es gibt erschiedene Aufgabentypen, die hier kurz vorgestellt sind.
4 Aufgabentypen
◦ a) Endliche Einzelfläche auf einer Seite der x-Achse: => bestimmtes Integral
◦ b) Endliche Teilflächen über und unter der x-Achse => Flächenbilanz
◦ c) Endliche Teilflächen über und unter der x-Achse => Flächenbetrag
◦ d) Unendliche Flächen mit Asymptoten => uneigentliches Integral
a) Einzelfläche
◦ Man berechnet das bestimmte Integral von a bis b:
◦ Man hat eine linke und eine rechte Integrationsgrenze, auch Rand genannt.
◦ Der Graph verläuft dort ganz unterhalb- oder ganz oberhalb der x-Achse.
◦ Man sucht den Flächeninhalt dieser einzelnen Fläche.
◦ Der Rechenweg steht unter => bestimmtes Integral berechnen
b) Teilflächen als Flächenbilanz
◦ Man berechnet das bestimmte Intergral von a bis b:
◦ Das kleine a ist die linke Integrationsgrenze und b die rechte.
◦ Der Graph verläuft dort teilweise über und teilweise unter der x-Achse.
◦ Der Graph hat damit immer auch mindestens eine Nullstelle.
◦ Die Nullstellen sind die Grenzen zwischen den Teilflächen.
◦ Man sucht die sogenannten Bilanz aller Flächen des Graphen:
◦ Flächen über der x-Achse sollen positiv gerechnet werden.
◦ Flächen unter der x-Achse sollen negativ gerechnet werden.
◦ Positive und negative Flächen gleichen sich also gegenseitig aus.
◦ Ein Integral berechnet automatisch immer diese Flächenbilanz.
◦ Siehe dazu unter => Flächenbilanz berechnen
c) Teilflächen als Flächenbetrag
◦ Man muss Teilflächen einzeln berechnen:
◦ Das kleine a ist die linke Integrationsgrenze und b die rechte.
◦ Der Graph verläuft dort teilweise über und teilweise unter der x-Achse.
◦ Der Graph hat damit immer auch mindestens eine Nullstelle.
◦ Die Nullstellen sind die Grenzen zwischen den Teilflächen.
◦ Man sucht die tatsächliche größe aller Flächen als eine positive Zahl.
◦ Alle Flächen - auch solche unterhalb der x-Achse - gelten als positiv.
◦ Fächen oberhalb und unterhalb der x-Achse werden einzeln berechnet.
◦ Siehe unter => Flächenbetrag berechnen
d) Unendliche Flächen als uneigentliches Intergral
◦ Der Graph von f(x) verläuft irgendwo auch asymtpotisch.
◦ Das heißt: er nähert sich einer Geraden immer mehr an.
◦ Dadurch können unendliche lange Flächenstücke entstehen.
◦ Siehe dazu unter => uneigentliches Integral
Herleitung: Säulenmethode
Alle Methoden der Integralrechnung beruhen letzten Endes auf der Einteilung der Fläche in viele - unendlich viele - schmale senkrechte Säulen, man spricht auch von der Säulenmethode. Zur praktischen Berechnung ist die Säulenmethode meist nicht nötig. Man verwendet vereinfachte Aufleitungsregeln. Zum Grundgedanken der Integralrechnung siehe unter => Säulenmethode
