Charakteristische Punkte
Mathematik
© 2016
- 2025
Definfition
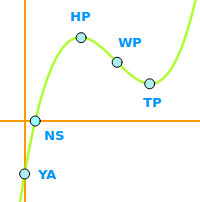
Charakteristisch nennt man besondere Punkte von Funktionsgraphen: y-Achsenabschnitte, Nullstellen (auch doppelte und dreifache), Hoch-, Tief-, Wende- und Sattelpunkte. Diese sind hier kurz vorgestellt.
Hintergrund
- Bei einer Kurvendiskussion bestimmt man charakteristische Eigenschaften eines Graphen.
- Das sind zum Beispiel Steigungen, Grenzwertverhalten, Symmetrien oder auch Krümmungen.
- Die wesentlichen Charakteristika sind oft aber bestimmte Punkte.
- Diese sind mit chararkteristischen Punkten gemeint.
- Siehe auch 👉 Kurvendiskussion
Liste charakteristischer Punkte
- Schnittpunkt mit x-Achse 👉 Nullstelle
- Schnittpunkt mit y-Achse 👉 Y-Achsenabschnitt
- Höchster Punkt, Gipfel 👉 Hochpunkt
- Tiefster Punkt, Talsohle 👉 Tiefpunkt
- Hoch- oder Tiefpunkt 👉 Extrempunkt
- Krümmung ändert sich 👉 Wendepunkt
- Wendepunkt mit Steigung Null 👉 Sattelpunkt
- Immer auch Extrempunkt 👉 Doppelnullstelle
- Immer auch Sattelpunkt 👉 Dreifachnullstelle
Sonderfälle
- x nicht defniert 👉 Definitionslücke
- Unendlichkeitsstelle 👉 Polstelle
- Enger werdende Wellen 👉 Oszillationsstelle
Wie bestimmt man sie?
- Die Bestimmung dieser Punkte ist normalerweise Teil der 👉 Kurvendiskussion
- Hier sind Links auf die üblichen Verfahren: