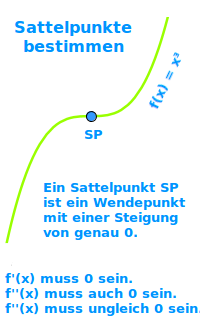
Sattelpunkte bestimmen
Anleitung
Basiswissen
Ein Sattelpunkt ist ein Wendepunkt bei dem zusätzlich noch die Steigung gleich 0 ist. Hier werden zwei Methoden zur Bestimmung vorgestellt.
Was meint Sattelpunkt hier?
- Ein Sattelpunkt ist ein Punkt auf dem Graphen einer Funktion.
- Ein Sattelpunkt ist ein Wendepunkt mit der Steigung Null.
- Wendepunkt meint: die zweite Ableitung muss Null sein.
- Steigung Null meint: die erste Ableitung muss Null sein.
- An der Stelle wechselt die Krümmung (immer).
- SP ist hier die Abkürzung.
Hinreichende Bedingung
- f'(x) = 0 UND
- f''(x) = 0 UND
- f'''(x) <> 0
Über Ableiten
- Bilde die erste Ableitung f'(x).
- Bilde die zweite Ableitung f''(x).
- Bilde die dritte Ableitung f'''(x):
- Setze f'(x) = 0, gibt mögliche SP
- Setze gefundene x-Werte in f''(x) ein.
- Wenn f''(x) auch gleich Null, dann sind SP weiter möglich.
- Setze mögliche x-Werte in f'''(x) ein.
- Wenn f'''(x) dann ungleich Null ist ...
- Dann gehört der x-Wert zu einem SP.
- x-Wert in f(x) einsetzen gibt den ...
- dazu passenden y-Wert.
Über Dreifachnullstelle
- Jede Dreifachnullstelle eines Graphen ist automatisch ein Sattelpunkt.
- Aber: nicht jeder Sattelpunkt ist eine Dreifachnullstelle.
- Dreifachnullstellen kann man am Funktionsterm erkennen.
- Mehr unter Dreifachnullstelle ↗
