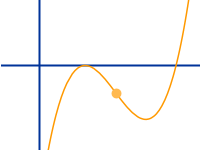
Wendepunkt
Analysis
Definition
Ein Wendepunkt ist ein Punkt auf dem Graphen einer Funktion. An dem Punkt muss sich die Richtung der Krümmung des Graphen ändern und zwar entweder von linksgekrümmt nach rechtsgekrümmt oder von rechtsgekrümmt nach linksgekrümmt. Eine übliche Abkürzung ist WP.
Was heißt Krümmung?
Geht man auf einem Graphen von links nach rechts entlang und macht man dann gedanklich eine Linkskurve, ist der Graph dort linksgekrümmt. Dort wo man sich auf einer Rechtskurve bewegt, ist der Graph rechtsgekrümmt. Am Wendepunkt wendet sich diese Krümmung von links nach rechts oder von rechts nach links. Lies mehr zu anschaulichen Beschreibung unter Krümmung ↗
Ist ein Sattelpunkt ein WP?
- Ja, immer: ein Sattelpunkt ist ein Wendepunkt mit der Steigung 0.
- Jeder Sattelpunkt ist automatisch auch ein Wendepunkt.
- Aber nicht jeder WP ist automatisch auch ein SP.
- Siehe auch Sattelpunkt ↗
Was wären keine Wendepunkte?
- Ein Punkt, bei dem die Krümmung von links auf Null wechselt (echte Kurve zu Gerader)
- Ein Punkt, bei dem die Krümmung von rechts auf Null wechselt (echte Kurve zu Gerade)
- Ein Punkt, bei dem zwar die Krümmung zwischen rechts und links wechselt, der aber einen Knick hat.
- Ein Punkt, bei dem zwar die Krümmung zwischen rechts und links wecheslt, der aber eine Definitionslücke ist.
Am Wendepunkt ist die Steigung extremal
- Man sagt, dass an einem WP die Steigung, also die Änderungsrate von f(x) oder y, extrem sei. Sie ist dann entweder extrem groß (sehr steil bergauf oder sehr steil bergab), oder sie ist extrem klein, also sehr "flach". Extrem groß ist die Steigung bei einem Links-Rechts-Wendepunkt. Links davon herrscht Linkskrümmung, rechts davon Rechtskrümmung. Extrem klein ist die Steigung einem Rechts-Links-Wendepunkt, wenn also links vom Wendepunkt Rechtskrümmung herrscht und rechts vom Wendepunkt Linkskrümmung.
Eigenschaften eines Wendepunktes
- Wendepunkte zählen nicht zu den Extrempunkten.
- Der x-Wert eines Wendepunktes heißt Wendestelle ↗
- Der y-Wert eines Wendepunktes heißt Wendewert ↗
- Die Tangente am Wendepunkt heißt Wendetangente ↗
- Ein Wendepunkt mit Steigung 0 heißt Sattelpunkt ↗
- Der Graph wechselt von einer auf die andere Tangentenseite.
- An einem WP sind alle Steigungen (außer unendlich) erlaubt.
- An einem WP ist die Steigung extrem (groß oder klein).
- Die Erste Ableitung f'(x) hat dort ein Extremum ↗
- Die zweite Ableitung f''(x) muss dort Null sein.
- Die dritte Ableitung f'''(x) kann 0 sein, muss es aber nicht.
- Ist die dritte Ableitung f'''(x) < 0 ist es ein LR-Wendepunkt ↗
- Ist die dritte Ableitung f'''(x) > 0 ist es ein RL-Wendepunkt ↗
- Siehe auch dritte Ableitung gleich null ↗
Wie bestimmt man einen Wendepunkt?
Am Graphen kann man ihn durch Hinsehen oft gut erkennen. Über die zweite Ableitung f''(x) kann man ihn auch berechnen: wo f''(x) zu 0 wird kann ein Wendepunkt vorliegen. Lies mehr unter Wendepunkte bestimmen ↗
