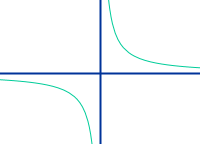
Umgekehrt proportional
Mathematik
Zwei Größen, oft x und y genannt, sind zueinander umgekehrt proportional wenn zwei zusammengehörige Zahlen immer dasselbe Produkt (Malrechnen) ergeben. Das ist ausführlich erklärt im Artikel => umgekehrte Proportionalität
Genau andere Reihenfolge
Das Wort „Rot“ ergibt umgekehrt geschrieben „Tor“. Umgekehrt heißt: die Reihenfolge genau andersherum machen. => Ganzen Artikel lesen …
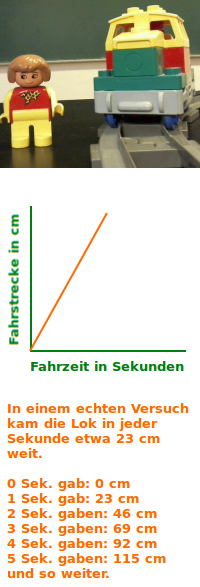Proportional
Zwei Größen wachsen und schrumpfen miteinander
Zwei Größen sind proportional zueinander, wenn eine Verdopplung der einen Größe automatisch auch die andere Größe mit verdoppelt. Beispiel: wenn eine Spielzeuglok doppelt so lange fährt, dann kommt sie auch doppelt so weit. Fahrzeit und Fahrstrecke sind zueinander proportional. => Ganzen Artikel lesen …
Stark
Jedes Jahr wächst die Jahreszahl seit Christi Geburt um eins an. Man kann für jedes Jahr dann bestimmen, wie viel Eis in der Antarktis abgebaut ist. Wenn diese Menge mit jedem Jahr um den gleichen Betrag steigt, würde man das Wachstum proportional nennen. Würde die abgetaute Menge pro Jahr aber mit jedem Jahr steigen, wäre es überproportional. Hier steht als Beispiel der Eisverlust in der Antarktis. => Ganzen Artikel lesen …
Mathematik
=> Ganzen Artikel lesen …
Definition
Brasilianer mit brauner oder schwarzer Hautfarbe sind im brasilianischen Parlament unterproportional vertreten. Das heißt: der Anteil dunkelhäutiger Personen ist im Parlament kleiner als in der Bevölkerung. Das Wort unterproportional ist hier kurz erklärt. => Ganzen Artikel lesen …
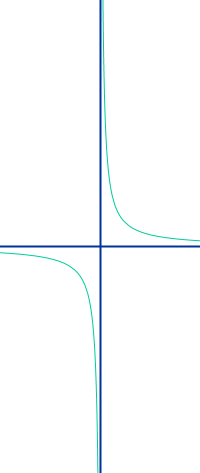Umgekehrt proportionale Funktion
f(x)=a/x
f(x) = a/x ist die allgemeine Form einer umgekehrt proportionalen Funktion. Man spricht auch von einer umgekehrt proportionalen Zuordnung [1] oder einer antiproportionalen Zuordnung. Jede Funktion, die man in diese Form umwandeln kann, ist umgekehrt proportional. Als Funktionsterm hat man eine Zahl geteilt durch x. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Physik
Mit diesem einseitigen Hebel als Tischversuch kann man einige Eigenschaften einer proportionalen Funktion am Beispiel von Kräften in Newton gemessen betrachten. Umgekehrt propotional zugeordnet sind hier die Entfernung der Bohrung vom Drehpunkt und die nötige Kraft, um den Balken in der Waage zu halten. => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
Beispiel
f(x) = 40/x oder f(x) = 1/x sind beides Beispiele für eine proportionale Funktion. Sie können nicht direkt über die Potenzregel abgeleitet werden, sie müssen vorher so umgeformt werden, dass das x im Zähler (oben) steht. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => umgekehrt proportionale Gleichung aus Versuch
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
Beispiele
Wenn sich der x-Wert verdoppelt, dann halbiert sich der y-Wert: das ist das Erkennungsmerkmal einer umgekehrt proportionalen Funktion. Das ist gleichbedeutend mit der Aussage, dass das Produkt aus x und y immer denselben Wert ergibt, also konstant ist. Der dazugehörige Graph ist eine Hyperbel. Hier stehen einige Beispiele als Gleichungen sowie auch Sachthemen (Hebel, elektrische Spannung, Rechteckflächen etc.). => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
Umgekehrt proportionale Gleichung
Definition
Siehe auch => Ganzen Artikel lesen …
… siehe unter => Proportionale Gleichung aus Versuch
Umgekehrt proportionale Gleichung aus Versuch
Lernwerkstatt
Angeleitete Werkstattversuche zum Selbermachen: einfache Versuch, die man oft in wenigen Minuten durchführen kann, und deren Auswertung dann als Funktionsgleichung eine umgekehrt proportionale Gleichung ergibt. Dazu stehen hier einige bewährte Beispiele aus einer Lernwerkstatt in Aachen. => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
Beispiele
Umgekehrt proportional nennt man Gleichungen, bei denen die Unbekannte, oft ein x, im Nenner eines Bruches erscheint. Hier stehen kurz aufgelistet einige Beispiele. => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
Rechenbeispiele
20/x = 4/2: das x steht im Nenner eines Bruches, also unten. Die Lösungsidee ist es, das x vom Nenner (unten) nach oben in den Zähler zu bringen. Das ist hier mit Beispielen kurz erklärt. => Ganzen Artikel lesen …
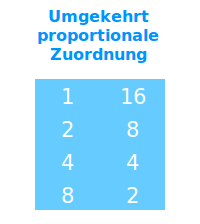Umgekehrt proportionale Zuordnung
… das Thema steht unter => umgekehrt proportionale Funktion
… meint dasselbe wie => Umgekehrt proportionale Funktionen
Doppelt so viel vom Einen gibt halb so viel vom anderen
Ein gutes Beispiel für diese Art von Dreisatz ist der Zusammenhang von Geschwindigkeit und Reisezeit. Wenn ich doppelt so viel „Geschwindigkeit habe“, dann gibt das nur „halb so viel“ Reisezeit. => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
