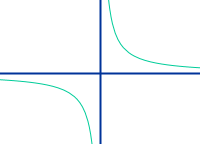
Umgekehrt proportional
Mathematik
© 2016
- 2025
Grundidee
Zwei Größen, oft x und y genannt, sind zueinander umgekehrt proportional wenn zwei zusammengehörige Zahlen immer dasselbe Produkt (Malrechnen) ergeben. Das ist ausführlich erklärt im Artikel 👉 umgekehrte Proportionalität
Fußnoten
- [1] Der Bronstein definiert: "Die Funktion y=a/x auch umgekehrte Proportionalität genannt, liefert eine gleichseitige Hyperbel, deren Asymptoten die Koordinatenachsen sind." In: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Dort die Seite 67.