Anschaulich
Das Verhältnis von zwei Zahlen sagt anschaulich, wie viel mal so groß die erstgenannte Zahl im Vergleich zur zweitgenannten Zahl ist. Das Verhältnis zweier Zahlen fasst die Ideen Anteil und Vielfache in einem Begriff zusammen. Hier werden kurz die Berechnung und anschauliche Bedeutung erklärt. => Ganzen Artikel lesen …
Arten
Als Verhältnis bezeichnet man jede Zahl, die ursprünglich aus einem Bruch oder einem Quotienten entstanden ist und angeben soll, wie viel mal so groß eine Sache ist, wie eine andere. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
… ein Wort wie „über“ oder „nach“, mehr unter => Lagewort
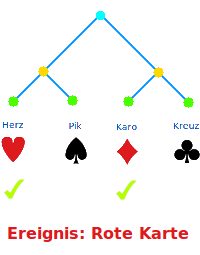Ereignis
Übersicht
Das Wort Ereignis wird sowohl in der Stochastik, also dem Rechnen mit Wahrscheinlichkeiten, wie auch in der Physik verwendet. In einem Lexikon aus dem Jahr 1793 ist ein Ereignis noch ganz allgemein eine Begebenheit. [1] Später wird noch recht vage ergänzt, dass ein Ereignis etwas ist, dass die Aufmerksamkeit auf sich zieht. [2] Eine Einengung dieser doch recht weiten Bedeutung erfuhr das Wort dann später in der Stochastik und der Physik. => Ganzen Artikel lesen …
Statistik
Es macht macht Sinn, vom Dreifachen, der Hälfte oder von drei Vierteln eines Wertes zu sprechen: Temperaturen in Kelvin eingeordnete ergeben eine Verhältniskala. Das ist hier für die Statistik kurz erklärt. => Ganzen Artikel lesen …
Psychologie
Männer neigen umso mehr zur Selbstüberschätzung, je kleiner ihr Zeigefinger im Verhältnis zu ihrem Ringfinger ist. Bei Frauen scheint der Effekt umgekehrt zu sein. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… siehe unter => ähnliche Dreiecke über Seitenverhältnisse
Erkennen
Wie man die Ähnlichkeit von zwei Dreiecke damit überprüft, dass man nur Seitenlängen misst, also keine Winkel. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
Was die Worte meinen
Bei einem Anteil sagt man, welchen Bruchteil vom Ganzen man meint. Beispiel: => Ganzen Artikel lesen …
Der Unterschied von zwei Zahlen
Das arithmetische Verhältnis sagt mir, um wie viel eine Zahl größer oder kleiner ist als eine andere Zahl. Die dazugehörige Rechnung ist das Abziehen. In welchem (arithmetischen) Verhältnis steht die 10 zur 7? Die 10 ist drei mehr als die 7, also ist das arithmetische Verhältnis von 10 zur 7 die Zahl 3. Bei einer Division (teilen) hingegen bildet man ein => geometrisches Verhältnis
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… veraltet für => umgekehrt proportionaler Dreisatz
… doppelt so viel x gibt auch doppelt so viel y, siehe unter => proportionaler Dreisatz
… doppelt so viel x, halb so viel y, siehe unter => umgekehrt proportionaler Dreisatz
Lösungsschema für proportionale Dreisatzaufgaben
Beim proportionalen Dreisatz funktioniert der Spruch: wenn das eine doppelt so viel wird, wird auch das andere doppelt so viel. Immer wenn das geht, kann man den Dreisatz über eine Verhältnisgleichung lösen. Diese Lösungsmethode kannst du verwenden, wenn du einfache Verhältnisgleichungen schon lösen kannst. Wenn du das noch nicht kannst, dann suche dir ein anderes Verfahren (es gibt mehrere). => Ganzen Artikel lesen …
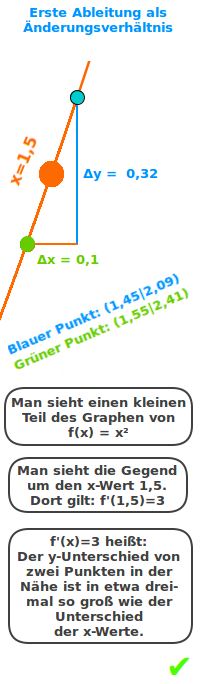Erste Ableitung als Änderungsverhältnis
f'(x) anschaulich
Den Wert einer ersten Ableitung kann man graphisch und im Sachkontext auf verschiedene Weisen deuten. Eine Deutung ist: wie viel mal so stark ändert sich y wie x. Dazu werden hier auch praktische Versuche vorgestellt. => Ganzen Artikel lesen …
… meint meistens das => 2D:4D-Verhältnis
… aus der Psychologie und Statistik => 2D:4D-Verhältnis
Vergleich über Vielfache oder Bruchteile
Das geometrische Verhältnis zwischen zwei Zahlen oder Mengen sagt mir, wie viel vom einen genauso viel ist wie das andere. Die dazugehörige Rechenart ist das Teilen. => Ganzen Artikel lesen …
Gleitverhältnis
Fliegerei
Das Gleitverhältnis ist der Kehrwert der Gleitzahl E. Es entspricht dem Höhenverlust bei einem Meter Vorwärtsflug. Es entspräche sinngemäß dem Betrag der Steigung einer Geraden. Hier steht eine Formel zur Berechnung. => Ganzen Artikel lesen …
… siehe unter => Gleitzahlen [Liste]
… siehe => Verhältnisfrage
… siehe => Verhältnisfrage
Versuch
20 bis 40 Minuten: für diesen Versuch brauchst du einen einfachen Taschenrechner. In der Kiste 4 findest du einige Messlöffel. Man kann sie in einem Haushaltswarenladen kaufen. Die Löffel hier kommen aus dem „Haus der Küche“. Auf dem Löffelstiel steht geschrieben, wie viel in die Löffel hineingeht. 15 ml heißt, dass der Löffel 15 Milliliter fasst. => Ganzen Artikel lesen …
Chemie
In Luft auf der Erde gibt es von der Masse, also der Kilogrammzahl her, etwa 3,27 mal so viel Stickstoff wie Sauerstoff. Das Massenverhältnis von Stickstoff zu Sauerstoff ist 3,27. Man kann das Massenverhältnis ohne Einheiten schreiben, oder auch mit immer zwei gleichen Einheiten, z. B. 3,27 g/g im Beispiel für Stickstoff zu Sauerstoff in der Luft. Das Formelzeichen ist das kleine griechische Zeta ζ. Hier steht noch ein Beispiel dazu. => Ganzen Artikel lesen …
ist richtig geschrieben. Eine häufige Falschschreibung ist: Preis-Leistungsverhältnis
Mathematisch
Die Seitenlänge 12 ist das Anderthalbfache oder das 1,5-fache von der Seitenlänge 8. Wie viel mal so lang eine Seite ist wie die andere nennt man das Verhältnis der Seiten, genauer wäre noch: das Verhältnis der Seitenlängen. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… meint in der Statistik dasselbe wie => Verhältnisskala
