Vektor
↗ Definition
Als Vektor bezeichnet man in der Mathematik oft einen Pfeil in einem 2D- oder 3D-Koordinatensystem. Er wird oft mit zwei, drei oder auch mehr Zahlen - den Vektorkoordinaten - geschrieben. Diese Zahlen sagen nichts darüber aus, wo ein Vektor in einem Koordinatensystem liegt. Die Zahlen sagen nur, wie lang der Vektor ist und in welche Richtung er zeigt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… 🍕 Torten- oder pizzastückartiges Kreisteil, heißt auch => Kreisausschnitt
Als Sektor bezeichnet man ganz allgemeinen einen Ausschnitt, also ein herausgenommenes Teil von etwas Ganzen. In der Geometrie steht der Begriff meist im Zusammenhang mit Kreisen und bezeichnet dann einen Kreissektor oder auf Deutsch => Kreisausschnitt
Technik
In der Technik ist ein Aktor ein Gerät, das ein Signal (elektrisch, pneumatisch, mechanisch) von einer Steuereinheit (z. B. Microcontroller, Computer) in eine Veränderung der physikalischen Welt umsetzt. Typische solche Aktoren sind Motoren, Schieber in Leitungssystemen, Heiz- oder Kühlemente, Lautsprecher oder Geräte zur Änderung von Drücken. In der Biologie nennt man einen Aktor einen => Effektor
… als griechische Silbe => außen
⊗☉↗⮅ Arten und Einteilung
Vektoren sind gedachte Pfeile in einem 2D-, 3D- oder höherem Koordinatensystem. Sie werden oft aus zwei oder drei Zahlen zusammengesetzt, etwa (4|3|5). => Ganzen Artikel lesen …
… auch Vektorkette genannt, die Summanden von einer => Vektorsumme
… Definition und Berechnung, siehe unter => Winkel zwischen Vektoren
… Definition und Berechnung, siehe unter => Winkel über Skalarprodukt
… Definition und Berechnung, siehe unter => Winkel zwischen Vektoren
… Definition und Berechnung, siehe unter => Winkel über Skalarprodukt
… siehe unter => Vektoranalysis
… Themenübersicht unter => Vektorrechnung
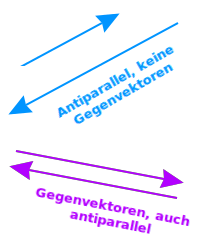Antiparallele Vektoren
⮂ Definition
⮂ Ein Vektor ist das (skalare) negative Vielfache des anderen Vektors: beide Vektoren sind damit auch parallel, sie zeigen mit ihren Pfeilspitzen aber in entgegengesetzte Richtung. [1]. Antiparallele Vektoren sind ein Sonderfall kollinearer Vektoren. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
… unterscheiden sich nur um negatives Vielfaches => antiparallele Vektoren
Definition
Als Vektorraum bezeichnet man eine Gesamtheit von Vektoren, die miteinander addiert, subtrahiert und die auch mit Zahlen multipliziert werden können. Als Basis eines solchen Vektorraums kann man jede beliebige Teilmenge defieren, also immer irgendwelche Vektoren, die man so als Linearkombination verbinden kann, dass man damit jeden anderen Vektor des gesamten Vektorraums darstellen kann. Das ist hier kurz mit einem Beispiel vorgestellt. => Ganzen Artikel lesen …
… siehe unter => Basis (Vektorraum)
… der Vektor (4|0|0) hat den Betrag 4, der Betrag ist gleich der => Vektorlänge
… Definition und Berechnung, siehe unter => Winkel zwischen Vektoren
… Definition und Berechnung, siehe unter => Winkel über Skalarprodukt
… für stochastische Prozesse siehe unter => Fixvektor
Übersicht
Ist das Ergebnis einer Subtraktion (Minusrechnung) ein Vektor, so kann man diesen Vektor als Diffferenzvektor bezeichnen. Eine Differenz ist eine Minusrechnung oder auch ihr Ergebnis. Im Zusammenhang mit Vektoren spielen zwei Fälle eine Rolle, die hier beide kurz vorgestellt sind. => Ganzen Artikel lesen …
Physik
Die Divergenz eines Vektorfeldes gibt für jeden Punkt des Feldes an, wie stark in seiner Umgebung die Vektoren auseinander streben. Die Divergenz selbst ist eine reine Zahl, also ein Skalar. Die Divergenz spielt unter anderem bei Strömungsfeldern und bei den Maxwell-Gleichungen der Elektrodynamik eine Rolle. => Ganzen Artikel lesen …
… siehe auch => Vektoren dividieren
Berechnung
Fügt man zwei Vektoren mit ihren hinteren Enden aneinander, spannen sie wie ein Buchstabe V ein Dreieck auf. Die dritte Seite ist dabei nicht sichtbar, aber ein Dreieck ist eindeutig bestimmt, wenn zwei der drei Seiten gegeben sind. Eine Formel berechnet direkt den Flächeninhalt. => Ganzen Artikel lesen …
… das wird behandelt im Artikel zu => Ebenengleichungen
… siehe unter => Parameterform der Ebene
… unterscheiden sich nur um positives Vielfaches => parallele Vektoren
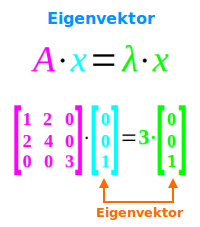Eigenvektor
Definition
A·x = λ·x: eine Matrix A wird mit einem Vektor x multipliziert. Wenn man die Matrix A durch eine reelle Zahl λ ersetzen könnte, ohne dass sich dadurch der Ergebnisvektor ändert, dann ist λ ein Eigenwert der Matrix A und x ein Eigenvektor dieser Matrix. [3] => Ganzen Artikel lesen …
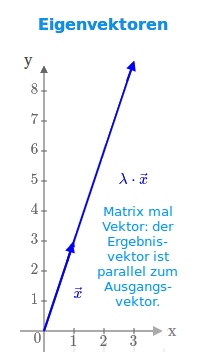Eigenvektoren
Beispiele
A·x = λ·x: jeder Vektor x der sich durch die Multiplikation mit einer Matrix A ledliglich in der Länge und eventuell Orientierung ändert aber noch parallel zum Ausgangsvektor x ist, heißt Eigenvektor. Hier stehen Beispiele dazu. Eine Definition steht unter => Eigenvektor
Matrizen
Matrix mal Vektor x = Vektor x mit neuer Länge, aber mit derselben Richtung. Die Orientierung darf eine anderere sein: „Zu einer Matrix A nennen wir v einen Eigenvektor und λ einen Eigenwert, wenn Av = λv erfüllt ist.“ [2][3] => Ganzen Artikel lesen …
Vektorrechnung
Ein Vektor, der senkrecht auf etwas steht (etwa einer Ebene) heißt Normalenvektor. Ein Vektor der genau die Länge eins hat, ist ein Einheitsvektor, auch normierter Vektor genannt. Ein Einheitsnormalenvektor ist also ein Vektor, der senkrecht auf etwas steht und genau die Länge 1 hat. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
