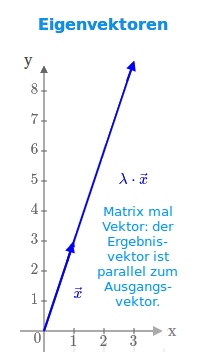
Eigenvektoren
Beispiele
© 2016
- 2025
Basiswissen
A·x = λ·x: jeder Vektor x der sich durch die Multiplikation mit einer Matrix A ledliglich in der Länge und eventuell Orientierung ändert aber noch parallel zum Ausgangsvektor x ist, heißt Eigenvektor. Hier stehen Beispiele dazu. Eine Definition steht unter 👉 Eigenvektor
Zur Schreibweise
- Matrix (a;b,c|d;e;f) heißt:
- a, b und c sind die Elemente der ersten Zeile (von links nach rechts).
- d, e und f sind die Elemente der zweiten Zeile (von links nach rechts).
Beispiel I
- Matrix: (3;0|-9;6)
- Eigenvektor: (1;3)
Beispiel II
- Matrix: (1;2;0|2;4;0|0;0;3)
- Eigenvektor: (0;0;1)
- Eigenvektor: eins durch Wurzel 5 mal (-2;1;0)
- Eigenvektor: eins durch Wurzel 5 mal (1;2;0)