Antiparallele Vektoren
⮂ Definition
Basiswissen
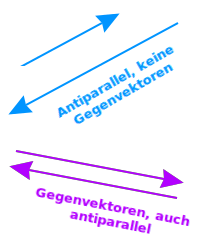
⮂ Ein Vektor ist das (skalare) negative Vielfache des anderen Vektors: beide Vektoren sind damit auch parallel, sie zeigen mit ihren Pfeilspitzen aber in entgegengesetzte Richtung.[1]. Antiparallele Vektoren sind ein Sonderfall kollinearer Vektoren. Das ist hier kurz erklärt.
Was meint skalar hier?
- Skalar meint hier: nur mit einer Zahl multipliziert.
- Bei Vektoren meint das: Jeder der Komponenten wird mit ein und derselben Zahl malgenommen.
- (Nicht skalar wäre die Multiplikation eines Vektors mit einem anderen Vektor.)
- Siehe auch Skalar ↗
Wie sind antiparallele Vektoren definiert?
- Kann man einen Vektor skalar mit einer negativen Zahl malnehmen, ...
- sodass als Ergebnis der andere Vektor herauskommt, dann heißen sie antiparallel.
- Beispiel das minus-Null-Komma-Achtfachte des einen Vektors gibt den anderen Vektor.
- Zwei antiparallele sind immer auch kollinear ↗
Welche geometrischen Eigenschaften haben antiparallele Vektoren
- Sie zeigen in genau entgegengesetzte Richtungen.
- Sie dürfen sich in ihrer Länge unterscheiden.
- Sind sie gleich lang, heißen sie auch Gegenvektoren ↗
Was meint parallel?
- Parallele Vektoren zeigen in genau dieselbe Richtungen.
- Sie unterscheiden sich nur in ihrer Vektorlänge ↗
Was ist der Gegenvektor?
Sind zwei Vektoren zueinander antiparallel und sind sie zudem auch noch gleich lang, das heißt sie haben denselben Betrag, dann ist der eine Vektor jeweils auch der Gegenvektor vom anderen[2]. Siehe auch Gegenvektor ↗
Was meint kollinear?
- Sowohl antiparallele als auch parallele Vektoren sind immer kollinear zueinander.
- Kollineare Vektoren haben entweder genau diesselbe oder genau entgegengesetzte Richtungen.
- Siehe auch kollinear ↗
Fußnoten
- [1] "Besitzen zwei Vektoren a und b entgegengesetze Richtung (Orientierung), so werden sie als zueinander antiparallel bezeichnet." Definition nach: Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Seite 47. In dieser Definition wird nichts über die Länge der betrachteten Vektoren gesagt oder damit auch nicht gefordert.
- [2] Definition nach: Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Seite 48.
