Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… Ein männliches Haus- oder Wildschwein. Das weibliche Tier heißt => Bache
… österreichisch für den Monat => Februar
Rechtschreibung
Überm wird korrekterweise ohne Apostroph geschrieben: „überm Himalaya-Gebirge ist die Luft sehr dünn“ ist also richtig geschrieben. Siehe auch => Apostroph
Rechtschreibung
„Sie sprang laut schreiend übers Bächlein.“ ist korrekt. Siehe auch => unters
… ist per Definition genau 1. Mehr unter => n über k
… ist genau 1. Mehr unter => n über k
Zeichnen
Man hat ein xy-Koordinatensystem und möchte darin einen 45°-Winkel ohne Geodreieck zeichnen. Hier steht eine kurze Anleitung dazu. => Ganzen Artikel lesen …
… über 0 ist per Definition immer genau 1. Mehr unter => n über k
Zeichentipp
Man kann einen exakten 90-Grad-Winkel auch ohne Geodreieck in einem Koordinatensystem zeichnen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
…. siehe unter => Orthogonalität überprüfen
… Formel und Herleitung unter => Kreisfläche aus Kreisumfang
… ein Å sind 10 hoch -10 Meter, mehr unter => Angström
Länge der Kathete a berechnen
Kennt man von einem rechtwinkligen Dreieck die Länge der Hypotenuse (längste Seite) sowie die Länge einer der beiden anderen Seiten (Katheten), kann man die Länge der dritten Seite (a) ausrechnen. Mehr über => Kathete über Pythagoras
… Formel und Herleitung unter => Kreisfläche aus Kreisumfang
Sekantenverfahren
Das Verfahren liefert die erste Ableitung an einem Punkt für eine Funktion, also f'(x). Gebräuchliche Namen sind auch Ableiten über den Differentialquotienten oder die h-Methode. Das Verfahren ist ausführlich beschrieben unter => Sekantenverfahren
… jedes Glied einzeln ableiten, mehr unter => Ableiten über Summenregel
… f(x)=5x³-x² gibt f'(x)=15x²-Siehe unter => ableiten über Summenregel
Anleitung
f(x) = 2·x³ wird abgeleitet zu f'(x) = 2·3·x². Der Faktor hier ist die Zahl 2 vor dem x³. Die allgemeine Regel dazu ist: a·g(x) ableiten gibt a·g'(x). Das heißt: ein konstanter Faktor a, der mit einem Term multipliziert wird, der x enthält, bleibt beim Bbleiten erhalten. Konstante Faktoren sind zum Beispiel alle reinen Zahlen und alle Terme, die man auf eine Zahl hin zusammenfassen kann. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… mit [f(x+h)-f(x)]Siehe unter => Sekantenverfahren
… siehe unter => ableiten über Umkehrregel
Ableiten über Kettenregel
Analysis
Die Funktion f(x)=(4x+2)³ gibt abgeleitet 4·3·(4x+2)². Die verwendete Regel war als Merkspruch: innere Ableitung (das gab hier die Zahl 4) mal äußerer Ableitung (das gab das 3·(4x+2)². Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …
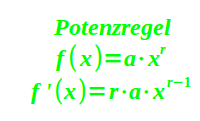Ableiten über Potenzregel
x² ⭢ 2x¹
x² gibt 2·x¹ oder kurz nur 2x: Exponent als Faktor runterziehen und eins kleiner machen. Beispiel: bei x³ ist der Exponent die Zahl 3. Diesen als Faktor (Malzahl) vor das x ziehen und dann den alten Exponenten eins kleiner machen: 3x². Als Regel: xʳ abgeleitet gibt r·xʳ⁻¹. Mehr unter => Potenzfunktion ableiten
Ableiten über Produktregel
Anleitung
f(x) = u·v gibt abgeleitet f'(x) = u'·v + u·v': u ist dabei die linke Seite von einem Malzeichen und v ist die recht Seite von einem Malzeichen. u und v können ein x enthalten oder auch nicht. Hat man einen Funktionsterm, bei dem das x auf zwei Seiten von einem Malzeichen steht, dann hat man eine sogenannte Produktfunktion und muss dann zwingend die Produktregel benutzen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
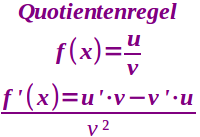Ableiten über Quotientenregel
Ist nötig, wenn x in Zähler und Nenner steht
Hat man einen Funktionsterm, bei dem das x sowohl im Zähler als auch im Nenner auftaucht, dann kann man die Quotientenregel benutzen. => Ganzen Artikel lesen …
Anleitung
f(x) = x² + 4x gibt abgeleitet f'(x) = 2x+4: die allgemeine Regel ist, dass man die Teile einer Plus- oder Minuskette, im Prinzip also die Summanden, für sich einzeln ableiten kann. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitung
f'(x) = 1:(f⁻¹)' abgeleitet. Diese Regel nennt man Inversenregel oder auch Umkehrregel. Sie ist hier kurz an einem Beispiel erklärt. => Ganzen Artikel lesen …
… f(x) gegeben, f-Strich von (x) skizzieren => Graphisch ableiten
… innen abgeleitetet mal außen abgeleitet => Ableiten über Kettenregel
… f(x) gegeben, f-Strich von (x) skizzieren => Graphisch ableiten
Anleitung
In einem xyz-Koordinatensystem sind ein Punkt (A|B|C) sowie eine Ebene in der hesseschen Normalenform x·n₀ = d gegeben. Eine einfache Formel berechnet den Abstand zwischen Punkt und Ebene. => Ganzen Artikel lesen …
Anleitung
In einem xyz-Koordinatensystem sind ein Punkt (A|B|C) sowie eine Ebene in Koordinatenform gegeben. Daraus kann der Abstand des Punktes von der Ebene leicht berechnet werden. => Ganzen Artikel lesen …
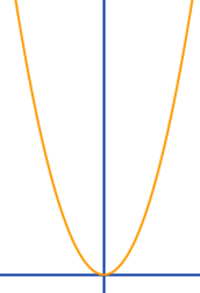Achsensymmetrie von Graphen überprüfen
Bedeutung | Methoden
Graphisch und rechnerisch: hier werden Methoden vorgestellt, wie man für eine gegeben Funktionsgleichung überprüft, ob der Graph achsyensymmetrisch zu y-Achse ist. => Ganzen Artikel lesen …
… 8 über 8 ist 0, siehe auch => n über k
… 8 über 18 ist 0, mehr unter => n über k berechnen
