Umkehrfunktion
x und y vertauscht
© 2016
- 2025
Basiswissen|
Kernidee|
Beispiel|
Anleitung|
Umkehrbarkeit|
Als Spiegelung|
Als Rotation|
Sinnbeispiel Tsunamiformel)|
Synonyme|
Fußnoten
Basiswissen
Die Variablen x und y vertauscht und dann nach x aufgelöst: so bildet man für eine gegebene Funktion f(x) die dazugehörige Umkehrfunktion f⁻¹ [2], auch inverse Funktion genannt. Diese Umwandlung ist aber nicht für alle Funktionstypen möglich. Hier stehen eine Anleitung sowie die anschauliche Bedeutung der Umkehrfunktion.
Kernidee
Die Kernidee einer Funktion f(x) ist es, dass man für jede erlaubte Zahl (also aus dem Definitionsbereich), die man für x einsetzt, eindeutig nur genau einen einzigen y-Wert oder Funktionswert f(x) als zugeordnete Zahl bekommt:
- f(x) = 4x+2
- f(5) = 4·5+2 = 22
Egal welche Zahl man in die Funktion f(x) einsetzt, wird man als Funktionswert immer nur genau eine einzige Zahl als "Ergebnis bekommen". Im Beispiel war das die Zahl 22. Es gibt aber auch Zuordungen, bei denen für eine eingesetzte x-Zahl, das sogenannte Argument (was man einsetzt), mehrere erlaubte zugeordnete Werte bekommt. Wenn das so ist, hat man keine Funktion mehr (muss eindeutig sein) sondern eine Zuordnung. Um das deutlich zu machen, schreibt man dann nicht mehr f(x) sondern y: [1]
- y² = x
Wenn man hier zum Beispiel für x die Zahl 4 einsetzt, kann man für y sowohl die -2 als auch die 2 einsetzen. Denn: 2·2=4 und auch (-2)·(-2)=4. Diese Gleichung ordnete also zumindest manchen x-Werten mehrere erlaubte y-Werte zu. Damit ist diese Zuordnung nicht eindeutig und somit auch keine Funktion.
Eine wichtige Frage für das Thema der Umkehrfunktion ist also immer: wenn man x und y vertauscht, entsteht dann aus der usprünglichen Funktion wieder eine Funktion (die eindeutig sein muss)? Und falls ja: wie sieht diese Funktion dann aus?
Beispiel
- Man hat y = 4x-12
- y meint dasselbe wie f(x).
- Man hat also f(x) = 4x-12
- Die Umkehrfunktion f⁻¹ ist dann f⁻¹(x) = 0,25+3
Anleitung
- Man vertauscht x und y in der Funktionsgleichung:
- Das gibt: x = 4y-12
- Dann nach y umstellen
- Das gibt y = 0,25x+3
- Das ist die Umkehrfunktion.
- Mehr unter 👉 Umkehrfunktion bestimmen
Umkehrbarkeit
- Nicht jede Funktion kann umgekehrt werden zu einer Umkehrfunktion.
- Zur Erinnerung: bei einer Funktion darf jeder x-Wert nur genau einen zugeordneten y-Wert haben.
- Das muss auch für die umgekehrte Funktion f⁻¹(x) gelten. Es gilt unter folgenden alternativen Voraussetzungen:
- Der Graph von f(x) ist streng motonon steigend oder ...
- Der Graph von f(x) ist streng monoton fallend.
- Oder kurz: der Graph ist 👉 streng monoton
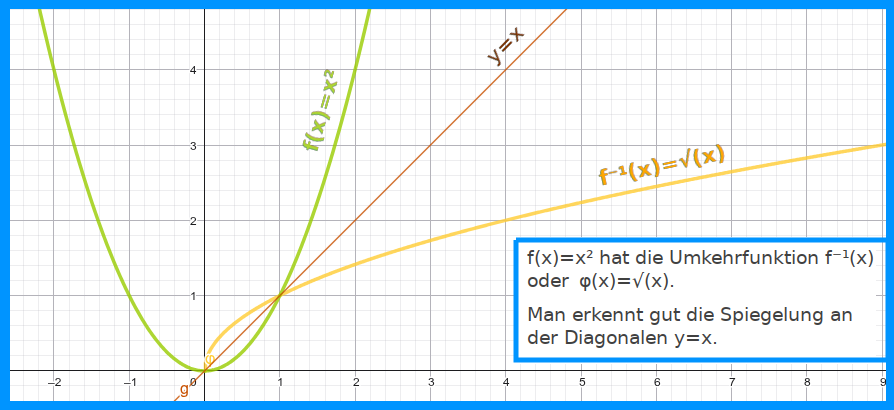
Als Spiegelung
- Anschaulich:
- Gegeben ist eine ursprüngliche Funktion f(x) mit dem Graphen.
- Man stellt man sich zusäztlich den Graphen einer Geraden g(x) = x vor.
- Der Graph von g(x) = x geht durch (0|0) und halbiert den Winkel zwischen x- und y-Achse.
- Man spiegelt jetzt den Graphen von f(x) an der Geraden g(x).
- Das Ergebnis ist der Graph der Umkehrfunktion f⁻¹.
- Siehe auch 👉 Achsenspiegelung
Als Rotation
- Anschaulich:
- Der Graph der Umkehrfunktion f⁻¹ kann auch durch eine gedachte Drehung erzeugt werden.
- Man stellt sich den Graph von f(x) auf eine Glasplatte gezeichnet vor.
- Die x-Achse liegt unten und geht von links nach rechts.
- Die y-Achse liegt links und geht von unten nach oben.
- Nun rotiert man die Platte so, dass die Achsen vertauscht werden.
- Die x-Achse geht jetzt mit steigenden Werten von unten nach oben.
- Die y-Achse geht jetzt mit steigenden Werten von links nach rechts.
- Abschließend vertauscht man die Beschrift der Achsen:
- Die untere horizontale Achse heißt wieder x-Achse.
- Die linke vertikal Achse heißt wieder y-Achse.
- Der jetzt sichtbare Graph ist der Graph von f⁻¹(x).
Sinnbeispiel Tsunamiformel)
Umkehrfunktion werden immer dann interessant, wenn man die Fragerichtung im Bezug auf x- und y-Werte umdrehen möchte. Nehmen wir als Beispiel die Tsunamiformel y = √(10·x). Das y steht hier für die Geschwindigkeit einer Tsunami-Welle in Metern pro Sekunde, das x für die Tiefe des Wasser in Metern. Die Tsunami-Formel ist ein typisches Beispiel für eine Wurzelfunktion.
y = √(10·x) mit y=f(x)
Man kann also fragen: wenn das Wasser die Tiefe x=1000 Meter (nicht besonders tief für Ozeane) hat, was ist dann die Geschwindigkeit des Tsunamis? Man setzt ein und rechnet: y = √(10·1000) und erhält für y den Wert 100. In 1000 Meter tiefen Wasser ist ein Tsunami dann rund 100 m/s oder gut 360 km/h schnell. Und welche Geschwindigkeit y ist der Wassertiefe 40 m zugeordnet? Die Funktion mit ihrer Funktionsgleichung ordnet dem x-Wert 40 m die Geschwindigkeit y = 20 m/s zu. Man kann nun immer weiter fragen, welcher Wassertiefe x welche Geschwindigkeit y gibt.
Umdrehung
Nun drehen wir die Richtung der Frage um: angenommen man hat gemessen, dass ein Tsunami eine Geschwindigkeit von 90 m/s hat. Wie tief wäre dann dort das Wasser? Man hat jetzt zuerst den y-Wert und fragt dann nach einem x-Wert. Zur Beantwortung dieser Art von Frage bildet man dann die Umkehrfunktion.
Umkehrfunktion
- y = √(10·x) mit y=f(x) | x und y vertauschen
- x = √(10·y) mit y=f⁻¹(x) | quadrieren
- x² = 10·y | durch 10
- y = 0,1x² | mit y=f⁻¹(x)
f⁻¹(x) = 0,1x² ist also die Umkehrfunktion. Das x steht jetzt nicht mehr für die Wassertiefe sondern für die Geschwindigkeit der Tsunami-Welle in Metern pro Sekunde. Und das y oder der Funktionswert steht dann für die Tiefe des Wassers in Metern. Probieren wir: wenn der Tsunami eine Geschwindigkeit von x = 90 m/s hat, setzen wir ein:
- y = 0,1·90² | ausrechnen
- y = 810
Von der Geschwindigkeit von 90 m/s als x-Wert kann man dann rechnerisch direkt auf die zugeordnete Wassertiefe y = 810 Meter schließen. Man sieht, die wie Umkehrung der Fragerichtung zur Idee der Umkehrfunktion führt.
Synonyme
Fußnoten
- [1] f(x) und y werden oft gleichbedeutend wie Synonyme verwendet. Möchte man aber zwischen eindeutigen Funktionen und mehrdeutigen Zuordnungen unterscheiden, dann nimmt man f(x) für die eindeutigen Funktionen und y für Zuordnungen die vielleicht eindeutig sein können, es aber nicht sein müssen. Mit dem y lässt man die Eindeutigkeit also offen. Siehe mehr unter 👉 f(x) oder y
- [2] "Umkehrfunktion, inverse Abbildung, Abbildung (Funktion), die eine gegebene Abbildung „umkehrt“, indem sie jedem Bildwert der Abbildung sein Urbild zuordnet. […] Ist g Umkehrabbildung von f, so schreibt man auch f⁻¹ anstatt g." In: Guido Walz: Spektrum Lexikon der Mathematik. Band 5: Sed bis Zyl; 2002; ISBN: 3-8274-9437-1. Dort der Artikel "Umkehrfunktion".