Bildinfo

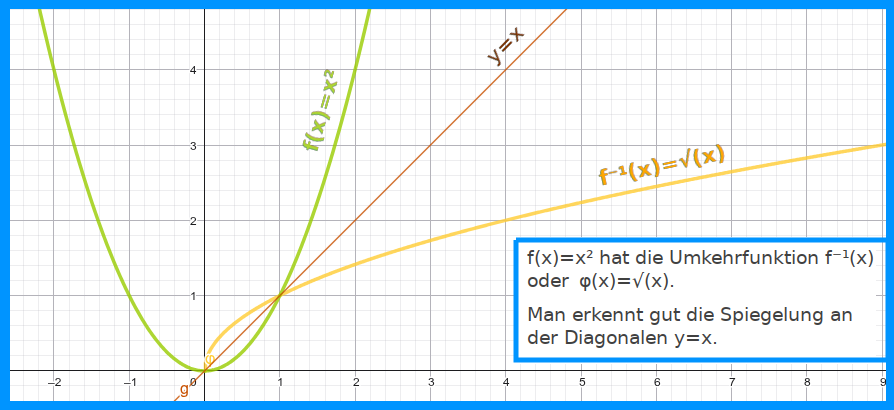
• Die Umkehrfunktion von f(x)=x² ist die Wurzelfunktion f⁻¹(x)=√. Beachte, dass graphisch die ursprüngliche Parabel nicht einfach an der Diagonalen y=x gespiegelt wird, sondern nur einer der zwei Äste der Parabel. Würde man die gesamte Parabel mit ihren beiden Parabelästen komplett spiegeln, gäbe es im resultierenden Graphen Punkte mit demselben x-Wert. Das aber ist für Funktionen nicht zulässig.

Source

• Created: November 17th, 2025
  

• Author: Gunter Heim
  

License

• This image is in the Public Domain.
  

Warranty

• No guarantee can be given as to the correctness of facts implied or explicitly stated.
  

• Usage is completey at your own risk. 💣
  

Originalseite

• Das Bild ist Teil eines online-Lexikons.
  

• Rhetos Lernlexikon Mathematik, Aachen:
  

• Siehe unter Umkehrfunktion ↗