Umfangsformeln
Liste
© 2016
- 2025
Kurzinfo
Der Umfang ist die Länge einer Randlinie. Bei einer Kugel ist Umfang etwas anders definiert. Hier stehen Formel zu einigen häufig vorkommenden geometrischen Figuren.
Rechteck
a+a+b+b: man addiert die Längen aller vier Seiten zusammen. Das Ergebnis ist der Umfang des Rechtecks. Da zwei gegenüberliegende Seiten immer gleich lang sind, kann man die Rechnung auch noch vereinfachen. Mehr unter 👉 Rechteckumfang
Quadratumfang
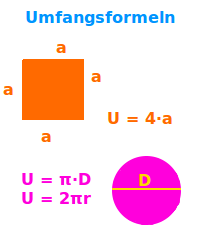
a+a+a+a oder kurz: 4·a - der Umfang eines Quadrates ist die Summer der Längen der vier Seiten. Da bei einem Quadrat die vier Seiten immer gleich lang sind, kann man auch kurz vier mal eine Seitenlänge rechnen. Mehr unter 👉 Quadratumfang
Dreieck
a+b+c: der Umfang eines Dreiecks ist gleich der Summe der Längen der drei einzelnen Seiten. Man addiert also die Längen der drei Seiten und das Ergebnis ist der 👉 Dreiecksumfang
Kreis
D·pi: multipliziert man den Durchmesser D eines Kreises mit der Kreiszahl pi (etwa 3,14) erhält man als Ergebnis den Umfang U des Kreises. Es gibt noch eine weitere Formel. Mehr unter 👉 Kreisumfang
Kugel
D·pi: der Umfang einer Kugel ist gleich dem Umfang des größten Kreises, den man auf die Kugeloberfläche zeichnen könnte. Lies mehr dazu unter 👉 Kugelumfang
Ellipse
Eine Ellipse ist eine Art langgezogener oder zusammengedrückter Kreis. Für eine Ellipse gibt es noch keine geschlossene Formel zur Berechnung des Umfangs. Es gibt nur Rechenwege für ungefähre Lösungen. Man spricht von Näherungslösungen. Mehr unter 👉 Ellipsenumfang