Schranke
Mathematik
Definition
Definition: Ein Zahlenwert, der nie über- oder unterschritten wird. Die Definition gilt bezieht sich auf die Elemente irgendeiner betrachteten Menge.
In welchen Zusammenhängen tritt der Begriff auf?
- Das Wort tritt auf im Zusammenhang mit
- einer Funktion ↗
- einer Folge ↗
- einer Reihe ↗
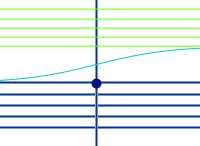
Was kann eine Schranke haben?
Der Begriff bezieht sich in der Mathematik immer auf eine Menge von Zahlenwerten. Eine solche Menge kann eine lose, ungeordnete Liste von Zahlen sein: Die Menge {3;7;2;8;5} hat die untere Schranke 2 und die obere Schranke 8. Bei Funktionen ist die betrachte Menge die Menge aller vorkommenden y-Werte (Bildmenge).
Wie ist Schranke definiert?
- Der Begriff gehört immer zu einer Menge von Zahlen.
- Wenn alle Elemente der Menge kleiner sind als eine bestimmte Zahl,
- dann ist diese bestimmte Zahl eine obere Schranke der Menge.
- Wenn alle Elemente der Menge größer sind als eine bestimmte Zahl,
- dann ist diese bestimmte Zahl eine untere Schranke der Menge.
Was wäre ein Beispiel?
- Angenommen man hat die Funktion f(x)=sin(x) ↗
- Bei dieser Funktion liegen alle y-Werte zwischen -1 und 1.
- Die Zahl 1 ist dann eine obere Schranke ↗
- Die -1 ist eine untere Schranke ↗
Welche Schranken werden unterschieden?
- Ein Wert, der nicht übertroffen wird heißt obere Schranke ↗
- Ein Wert, der nicht unterboten wird heißt untere Schranke ↗
- Supremum ist das Fremdwort für die kleinste obere Schranke ↗
- Infimum ist das Fremdwort für die größte untere Schranke ↗
Was ist der Unterschied zum Grenzwert?
- Bei einer Schranke betrachtet man alle vorkommenden y-Werte.
- Bei einem Grenzwert betrachtet man nur y-Werte in eine bestimmte x-Richtung.
- Beispiel: die Funktion f(x)=1/x hat als Graphen die Normalhyperbel ↗
- Die Funktion hat weder eine obere noch eine untere Schranke.
- Denn: nahe bei x=0 geht der Graph für y gegen plus unendlich und minus unendlich.
- Betrachtet man aber den Grenzwert für x gegen unendlich, dann ist dieser 0.
- Die Zahl 0 wäre aber keine Schranke der Funktion.
- Siehe auch unter Grenzwert ↗
Beispielhaft Aussagen zu Schranken
- Man hat die Menge aller reellen Zahlen größer 5 und kleiner 7.
- Folgende Aussagen sind dann wahr:
- 17 ist eine obere Schranke.
- 12 ist eine obere Schranke.
- 7 ist eine obere Schranke.
- 7 ist die kleinste obere Schranke, das Supremum ↗
- 0 ist eine untere Schranke.
- 3 ist eine untere Schranke.
- 5 ist eine untere Schranke.
- 5 ist die kleinste untere Schranke, das Infimum ↗
- Es gibt kein Maximum ↗
- Es gibt kein Minimum
