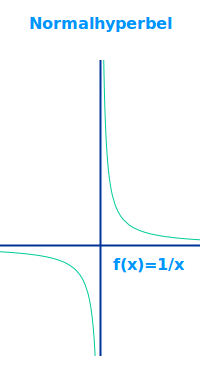
Normalhyperbel
f(x)=1/x
Definition
"Normalhyperbel" meint in Anlehnung an den Begriff der Normalparabel den Graphen der Funktion 1/x, sprich: Eins-durch-x. Der Graph ist hier mit seinen Eigenschaften kurz vorgestellt.
Koordinatensystem
Die x-Achse geht von links nach rechts, die y-Achse von unten nach oben. Man teilt das normale x-y-Koordinatensystem oft in vier Felder ein, die vier Quadranten: Oben rechts ist der erste Quadrant, oben links der zweite, unten links der dritte und unten rechts der vierte Quadrant. Siehe auch normales Koordinatensystem ↗
Zwei Äste
Die Normalhyperbel hat zwei Äste: einen im dritten Quadranten (unten links) und einen im ersten Quadranten (oben rechts). Man kann auch vom linken und vom rechten Ast sprechen. Der linke Ast hat negative x-Werte und negative y-Werte. Der rechte Ast hat positive x-Werte und positive y-Werte.
Linker Ast
Von links, also minus-unendlich kommend, läuft der Graph ganz knapp unterhalb der x-Achse. Die Funktionswerte sind alle negative Zahlen ganz nahe bei der Null. Je weiter man nach rechts Richtung y-Achse geht, desto "negativer" werden die Zahlen. Nahe der y-Achse stürzen sie nach unten ab. Wenn man mit x von links gegen 0 geht, gehen die y-Werte gegen minus-unendlich. Man sagt auch, der Graph nähere sich asymptotisch der y-Achse an. Siehe auch asymptotisch ↗
y-Achse
Für x=0 ist die Funktion nicht definiert. Der x-Wert 0 hat also keinen y-Wert. Es gibt deshalb auch keinen y-Achsenabschnitt. Man sagt, dass 0 eine Definitionslücke ist. Im Graphen nennt man solche Definitionslücken auch Polstellen ↗
Rechter Ast
Für sehr kleine positive x-Werte ist der Funktionswert sehr groß. Wenn man gedanklich von rechts kommend immer näher an die y-Achse geht, dann gehen die y-Werte gegen unendlich. Geht man nach rechts, gehen die y-Werte gegen 0. Der rechte Ast schmiegt sich also asymptotisch an die y-Achse und an die x-Achse an.
Zusammenfassung
- f(x) = 1/x
- y-Achsenabschnitt: gibt es nicht
- Nullstellen: gibt es nicht
- Tiefpunkte: gibt es nicht
- Hochpunkte gibt es nicht
- Wendepunkte: gibt es nicht
- Linker Ast (negative x-Werte): Rechtsgekrümmt
- Rechter Ast (positive x-Wert): Linksgekrümmt
- Symmetrie: punktsymmetrisch zum Ursprung
- Siehe auch Normalhyperbel Wertetabelle ↗
