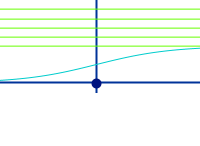
Obere Schranke
Jeder Wert, der nicht überschritten wird
© 2016
- 2026
Basiswissen
Kurz erklärt: kein Funktionswert beziehungsweise kein Element der betrachteten Menge ist größer als diese Zahl.
Erläuterung
Der Graph der Funktion f(x) = 1/ [1+e^(-x)] hat nirgends im Koordinatensystem Funktionswerte (y), die größer sind als 1. Damit ist die Zahl 1 eine obere Schranke der Funktion f(x). Auch die Zahlen 1,0001 oder 29 wären obere Schranken. Für eine ausführliche Definition siehe unter 👉 Schranke
Sachthemen
Die Ausbeutung geologischer Lagerstätten, etwa von Gas, kann nicht unbeschränkt nach oben wachsen. Irgendwann tritt die sogenannte Lagerstättenerschöpfung ein. Beispiele für sachlich begründete obere Schranken stehen unter 👉 nach oben beschränktes Wachstum