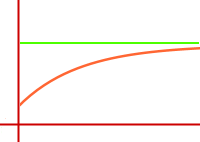
Nach oben beschränktes Wachstum
y-Wert hat obere Schranke
Basiswissen
Ein Funktionswert nimmt ständig zu, überschreitet aber niemals eine obere Grenze, den sogenannten Sättigungswert. Das wird hier kurz vorgestellt.
Sachbeispiele
Ein Baum wächst, kann aber eine maximale Höhe niemals überschreiten. Oder die Weltbevölkerung nimmt ständig zu, hat aber eine natürliche obere Grenze. Ausformulierte Beispiele stehen unter Nach oben beschränkte Wachstumsprozesse ↗
Mathematisch
Von einem Wachstum im engeren Sinn spricht man bei streng monoton steigenden Funktionen. Im erweiterten Sinn kann man auch leichte Abnahmetendenzen akzeptieren, im Endeffekt muss der Funktionswert aber für wachsenende x-Werte selbst auch größer werden.
Der Sättigungswert
Der Funktionswert, der niemals überschritten wird und - je nach Modell - oft nur als Grenzwert erreicht wird heißt Sättigungswert. Mathematisch spricht man auch von einen sogenannten Supremum. Das klassiche Beispiel für einen Sättigungswert ist eine kalte Tasse Wasser in einem warmen Raum. Das Wasser wird sich immer mehr der Raumtemperatur annäheren, diese aber niemals überschreiten. Siehe auch Sättigungswert ↗
Das Sättigungsmanko
Das ist die Differenz vom aktuell betrachteten Funktionswert (y-Wert) zum Sättigungswerte. Beträgt im Wasserglasbeipiel die Temperatur des Wassers gerade 18,5 Grad Celsius und liegt die Raumtemperatur bei 20 °C, dann ist das Sättigungsmanko 1,5 °C. Lies mehr dazu unter Sättigungsmanko ↗
Als Exponentialfunktion
- B(t) = S-(S-A)·e^(-k·t)
Legende
- B(t) = Bestand zum Zeitpunkt t
- S = Grenzwert, obere Schranke, Sättigungswert
- A = Anfangswert zum Zeitpunkt t=0
- e = Eulersche Zahl ↗
- k = Wachstumskonstante, k>0
- t = Zeit
Sachbeispiele
Algen vermehren sich in einem See: eine theoretische Obergrenze ist das Seevolumen. Oder: ein Baum wächst in die Höhe: eine natürliche Obergrenze bildet die Steigfähigkeit von Wasser in den Kapillarröhrchen. Weitere Beispiele stehen unter Nach oben beschränkte Wachstumsprozesse ↗
