Kartesische Form in Polarform
Umwandlung
© 2016
- 2025
Basiswissen
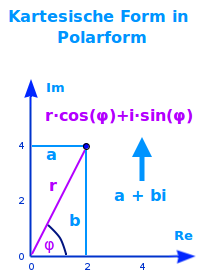
Die kartesische Form a+bi kann umgewandelt werden in die Polarform r·[cos(phi)+i·sin(phi)] einer komplexen Zahl. Das ist hier kurz erklärt.
Umwandlung
- Kartesische Form: a+bi
- Polarform: r·[cos(phi)+i·sin(phi)]
- r = √(a²+b²)
- phi = Arkustangens von b durch a
Legende
- r = Betrag der Zahl, Abstand zum Ursprung
- e = Eulersche Zahl, etwa 2,71828
- i = Imaginäre Einheit
- phi = Argument der komplexen Zahl
In Worten
Man hat eine komplexe Zahl in kartesischer Form a+bi. Man berechnet zuerst den Betrag r indem man a²+b² rechnet und aus dem Ergebnis die Wurzel zieht. Dann berechnet man den Winkel phi: man dividiert b durch a und nimmt davon den Arkustangens. Die Ergebnisse setzt man dann in die Polarform ein.
Die Umkehrung
Man kann auch umgekehrt eine Polarform umwandeln in die kartesische Form. Das ist erklärt unter 👉 Polarform in kartesische Form