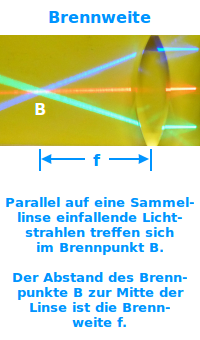
Brennweite
Physik
Basiswissen
Brennweiten werden angegeben für Parabolspiegel (auch Antennen) sowie auch für optische Linsen. Das Wort Brennweite alleine meint meistens die Brennweite einer Linse.
Die Brennweite eines Parabolspiegels
Ein Parabolspiegel ist ein konkav, das heißt nach innen gewölbter Spiegel dessen Form aus geeigneten Teilen einer mathematischen Parabel zusammengefügt werden kann. Lichtstrahlen, die parallel zueinander und parallel zur Symmetrieachse auf den Spiegel fallen, werden nach der Reflexion gemeinsam in einem Punkt zusammengeführt. Das ist Brennpunkt des Parabelspiegels. Zur geometrischen Definition der dazugehörigen Brennweite siehe unter Parabelbrennweite ↗
Definition der Brennweite für optische Linsen
Die Brennweite entspricht bei dünnen Der Abstand f einer Lupe (Sammellinse) zum heißesten Punkt: die Lupe führt parallel einfallende Lichtstrahlen auf der anderen Linsenseite in einem Punkt zusammen. Dadurch wird die Wärme des einfallenden Lichtes gebündelt. Bei Sonnenlicht wird dieser Punkt oft heiß genug, um im Brennpunkt ein Feuer zu entzünden. Die Brennweite
Definition für dünne Linsen
- Die Definition gilt für dünne bikonvexe Sammellinsen (Lupen):
- Eine bikonvenxe Linse hat eine Mittellinie bzw. Symmetrieachse.
- Das ist die Linie von der einen Spitze bis zur anderen Spitze.
- Die Mitte dieser Linie ist auch die Mitte der Lupe (Sammellinse).
- Man stellt die Lupe gedanklich senkrecht, also die Spitzen oben und unten.
- Eine waagrechte Linie durch die Mitte der Lupe heißt dann: optische Achse.
- Nun denkt man sich mehrere Lichtstrahlen parallel zur optischen Achse.
- Sie treffen von einer Seite aus kommend auf die Sammellinse.
- Auf der anderen Seite werden sie sich immer im Brennpunkt B treffen.
- Der Abstand des Brennpunktes B zur Mitte der Lupe ist die Brennweite f.
Ist die Brennweite unter Wasser eine andere?
- Ja und zwar immer eine größere:
- Die Brennweite hängt nicht nur vom Material der Lupe und dem Material ab.
- Die Brennweite hängt auch noch vom umgebenden Medium ab.
- Zur Herleitung, siehe unter Snelliussches Gesetz ↗
Welche Formeln spielen eine Rolle?
- Als Bedingung für eine scharfe Abbildung: 1/f = 1/b + 1/g Linsenformel ↗
- Zur rechnerischen Herleitung der Brennweite Snelliussches Gesetz ↗
Wie wird die Brennweite abgekürzt?
- Die Brennweite wird oft mit einem kleinen f abgekürzt.
- Man kann zum Beispiel schreiben: f = 20 cm
- (vom lateinischen Fokus)
Was besagt die Brennweite bei Lupen?
- Je kleiner die Brennweite, desto stärker die Vergrößerung.
- Man beachte: unter Wasser haben Lupen eine andere Brennweite als an Luft.
- Unter Wasser ist die Brennweite größer und der Vergrößerungseffekt kleiner.
- Siehe auch unter Lupe ↗
Wie bestimmt man die Brennweite praktisch?
- Man hält die Lupe in die Sonne.
- Man verändert die Lage der Lupe so lange, ...
- bis man auf einem Untergrund einen kleinen sehr hellen Punkt erkennt.
- Dabei soll die Lupe senkrecht zum einfallenden Licht gehalten werden.
- Der Abstand der Lupe zu dem kleinen hellen Punkt ist die Brennweite f.
- Achtung: der Punkt kann sehr heiß werden und ein Feuer entfachen.
Wie kann man die Brennweite noch bestimmen?
- Kauft man eine Lupe, ist die Brennweite oft eine Herstellerangabe.
- Bei manchen Lupen steht sie zum Beispiel auch mit auf dem Griff.
- Bei Brillengläsern (auch oft Lupen) sind oft Dioptrien angegeben.
- Der Kehrwert der Dioptrien ist wiederum die Brennweite f.
Was sind Dioptrien bei Brillen?
- Der Kehrwert der Brennweite heißt Brechkraft (oder Brechwert).
- Die Brechkraft wird in Dioptrien angegeben.
- Der Kehrwert der Dioptrien-Zahl ist die Brennweite.
- Bei Brillengläsern findet man oft Dioptrien.
- Eine Brille mit 1,5 Dioptrien hätte als Brennwert
- 1/1,5 oder etwa 0,67 Meter.
- Mehr unter Dioptrien ↗
Fußnoten
- [1] Definition über Glasmitte, 1793: "Die Brênnweite, plur. die -n, bey den optischen Gläsern, die Entfernung des Brennpunctes von der Mitte des Glases oder Spiegels. In: Adelung, Grammatisch-kritisches Wörterbuch der Hochdeutschen Mundart, Band 1. Leipzig 1793, S. 1188. Online: http://www.zeno.org/nid/20000088064
- [2] Definition über Glasmitte, 1854: "Brennweite, bei Linsengläsern und Hohlspiegeln die Entfernung des Brennpunktes von der Mitte des Linsenglases oder Hohlspiegels." In: Herders Conversations-Lexikon. Freiburg im Breisgau 1854, Band 1, S. 663. Online: http://www.zeno.org/nid/20003246868
- [3] Definition über scharfe Bilder,1857: "Brennweite, der Abstand des Brennpunktes vom Mittelpunkt eines Brennglases od. Brennspiegels. Durch die Erfahrung findet man die B. sphärischer Gläser, indem man sucht, in welcher Entfernung hinter dem Glase sich deutliche Bilder sehr entfernter Gegenstände entwerfen. Vgl. Brennglas u. Brennraum. In: Pierer's Universal-Lexikon, Band 3. Altenburg 1857, S. 283. Online: http://www.zeno.org/nid/20009586393
- [4] Definition über Hauptebenen, 1904: " Diese zwei Ebenen heißen die Hauptebenen des Systems, ihre Schnittpunke H und H' mit der Achse heißen die Hauptpunkte. Die Abstände der Brennpunkte von den Hauptpunkten H F = f und H' F' = f' heißen die Brennweiten des Systems." Was die Hauptebenen sind ist ausführlich im original Artikel erklärt. (Diese Definition verwendet auch gut 100 später noch das Spektrum Lexikon der Physik.) In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 6 Stuttgart, Leipzig 1908., S. 169-171. Online: http://www.zeno.org/nid/2000607720X
- [5] Definition über Formeln, 1905: "Brennweite, der Abstand des Brennpunktes vom optischen Mittelpunkt einer Linse oder eines sphärischen Spiegels. Bei einem sphärischen Hohlspiegel ist sie gleich dem halben Halbmesser der Kugel, von deren Oberfläche die Spiegelfläche ein Teil ist. Die B. einer Linse hängt von den Krümmungsradien der beiden Linsenflächen und von dem Brechungskoeffizienten der Substanz ab, aus der die Linse besteht. Bezeichnet man mit r und r' die Krümmungsradien, mit n den Brechungskoeffizienten und mit f die B., so hat man 1/f = (n-1)(1/r + 1/r'). Für eine gleichseitig-biconvexe Linse z. B. ist r' = r, demnach 1/f = 2(n-1)/r oder f = r/2(n-1). Besteht die Linse aus gewöhnlichem Glas, dessen Brechungskoeffizient = 3/2 ist, so ergibt sich f = r, d. h. bei einer gleichseitig-biconvexen Linse aus gewöhnlichem Glas ist die B. gleich dem Krümmungsradius einer Linsenfläche. Für eine ebensolche Flintglaslinse (n = 1,635) dagegen ergibt sich f = 0,787. r und für eine Linse aus Diamant (n = 2,487) nur f = 0,336. r. Für gleich geformte Linsen aus verschiedenen Substanzen wird die B. kleiner, wenn das Brechungsverhältnis des Materials zunimmt. Die Krümmungsradien konkaver Flächen sind bei Berechnung der B. negativ zu nehmen. Alsdann ergibt sich die B. der Hohllinsen negativ, entsprechend dem Umstande, daß Linsen dieser Art nur virtuelle Brennpunkte besitzen; vgl. Linse. Experimentell wird die B. bestimmt, indem man die Entfernung a eines Gegenstandes und die Entfernung b seines Bildes von der Linse oder dem Spiegel mißt und daraus die B. mit Hilfe der Gleichung 1/f = 1/a + 1/b berechnet. In: Meyers Großes Konversations-Lexikon, Band 3. Leipzig 1905, S. 390. Online: http://www.zeno.org/nid/20006367097
