Zweidimensional
2D
Wasserflächen, Quadrate, Kreise oder auch Kugeloberflächen sind typische zweidimensionale Objekte. Daneben spricht man auch von zweidimensionalen Funktionen. Hier stehen eine Definition sowie verschiedene Verwendungen des Wortes zweidimensional in der Mathematik. => Ganzen Artikel lesen …
Dreidimensional
3D
Kugeln, Körper an sich, der Raum: dreidimensional, kurz auch 3D heißt: räumlich im Gegensatz zu flach. Räumliche Dinge haben ein Volumen oder Rauminhalt (cm³). Das ist hier näher erklärt. => Ganzen Artikel lesen …
Eindimensional
1D
Eine Sache auf der man nur hin und her gehen kann nennt man eindimensional: auf einem Zahlenstrahl, einem Faden oder einer dünnen Linie kann man nur hin und dann auf derselben Linie wieder zurück gehen. Das wären damit Beispiele für eindimensionale Dinge. Präziser gesagt: ein Objekt ist mathematisch gesehen genau dann eindimensional, wenn man ein Koordinatensystem definieren kann, sodass zur eindeutigen Angabe eines beliebigen Punktes des Objektes nur genau eine relle Zahl nötig ist. Es folgen hier Bedeutungen in verschiedenen Fachgebieten. => Ganzen Artikel lesen …
Vierdimensional
Anschaulich
Man spricht in der Physik von einer vierdimensionalen Raumzeit oder auch vierdimensionalen Funktionen in der Mathematik. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… nicht flach, sondern auch räumlich, siehe unter => 3D
… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
.png "Die einfachste Version, um eine Abbildung der Art ℝ² ↦ ℝ geometrisch-anschaulich darzustellen.")
Pythagoreischer Aufzug (zweidimensionale Funktion)
Höhere Mathematik
Der pythagoreische [1] Aufzug ist die einfachere Variante zum pythagoreischen Flaschenzug. [2] Der Versuch wird hier so beschrieben, dass man ihn schnell mit einfachsten Haushaltsmitteln (Pappe, Reißzwecken/Nägel, Schnur/Seil) aufbauen kann. Mit einer sehr einfachen Mechanik kann man anschaulich zeigen, was eine zweidimensionale Funktion [3] und die Schreibweise ℝ² ↦ ℝ [4] bedeuten. => Ganzen Artikel lesen …
Analysis
Mit einer sehr einfachen Mechanik kann man anschaulich zeigen, was eine zweidimensionale Funktion und die Schreibweise ℝ² ↦ ℝ bedeuten. Für die hier beispielhaft zusammengestellten Zahlen kann man dann versuchen, eine passende Funktionsgleichung zu finden. => Ganzen Artikel lesen …
Hoch- und Tiefpunkte
Zweidimensional ist eine Funktion genau dann, wenn sie exakt zwei unabhängige Variablen hat. Ein Beispiel ist die Funktion f(x;y)=x²+y². Ihr Graph wird in einem 3D-Koordinatensystem mit x-, y- und z-Ache dargestellt. Der Graph ist hier eine nach oben geöffnete Schüssel mit dem tiefsten Punkt bei (0|0|0). Dieser Punkt ist also ein zweidimensionaler Tiefpunkt. Analog fasst man auch einen zweidimensionalen Hochpunkt. Lies mehr unter => zweidimensionale Extrempunkte berechnen
Kurzanleitung für f(x;y)
Zweidimensional nennt man Funktionen mit zwei unabhängigen Variablen. Ihre Graphen sind oft Flächen in einem 3D-Koordinatensystem mit x-, y- und z-Achse. Sie zu berechnen heißt, ihre x- und y-Werte zu rechnerisch zu bestimmen. Das Vorgehen ähnelt stark dem eindimensionaler Funktion mit f(x). Das Vorgehen ist hier kurz erläutert. => Ganzen Artikel lesen …
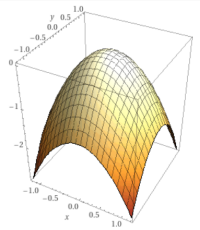Zweidimensionale Funktion
z=f(x;y)
Die Dimension einer Funktion entspricht der Anzahl der unahbängigen Variablen: zweidimensionale Funktionen, auch als Funktionen mit zwei veränderlichen [2], mit zwei Variablen [3] oder als bivariate Funktionen bezeichnet [3], haben dementsprechend genau zwei unabhängige Variablen, oft als x und y bezeichnet. Die dritte Variable, oft das z, ist von x und y abhängig und heißt auch Funktionsargument. Das ist hier näher erläutert. => Ganzen Artikel lesen …
Beispiele
Als zweidimensional bezeichnet man Funktionen, die zwei Argumente haben, also zwei Zahlen, die man in den Funktionsterm einsetzt. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
… meint eigentlich dasselbe wie => Kreis
… für x-, y- und z-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
… meint am ehesten ein => Rechteck
… meint eigentlich dasselbe wie ein => Quadrat
… oft mit großem C bezeichnet, mehr unter => Komplexe Zahl
… meint am ehesten die Grundfläche eines Zylinders, das ist immer ein => Kreis
… für x-, y- und z-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
… es gibt verschiedene => zweidimensionale Extrempunkte
Geometrie
Ein Torus ist ein dreidimensionaler Körper, ähnlich einem Rettungsring. Zweidimensional heißt flach, z. B. wie ein Blatt Papier. Eine flache Figur, die von der Form her an einen Torus erinnert ist der => Kreisring
… meint am ehesten die Grundfläche eines Zylinders, das ist immer ein => Kreis
… meint am ehesten die Grundfläche eines Trapez, das ist immer ein => Vieleck
