Unendlich
∞
Geht man auf dem Rand eines Kreises entlang, so hat dieser nie ein Ende, auch wenn man dabei immer wieder dieselben Punkte durchläuft. Der Kreisrand ist so gesehen unendlich. Das ist eine Bedeutung des Wort. Die andere Bedeutung geht davon aus, dass etwas unendlich großes endlos ist, ohne dass sich dabei dieselben Orte oder Zeiten wiederholen. Siehe mehr dazu unter => Unendlichkeit
Immer abends, was normalerweise abends kommt oder passiert
Endlich
Hört irgendwann mal auf
In der Mathematik meint man mit endlich oft, dass eine Menge nur eine begrenzte Anzahl hat. Eine endliche Menge wäre die Menge der Monate, deren Namen auf r endet. Eine unendliche Menge wäre die Menge der natürlichen Zahlen. Von denen gibt es gedanklich unendlich viele. Neben dieser Bedeutung von endlich gibt es noch eine andere. => Ganzen Artikel lesen …
♂ ein Mann oder Junge seiend
… geht nicht, mehr dazu unter => Genau Pi
Stündlich
Immer einmal in jeder Stunde
Stündlich heißt, dass etwas im Abstand von einer Stunde immer wieder neu beginnt. Eine stündliche Radiomeldung zum Beispiel könnte immer zur vollen Stunde beginnen. Siehe auch => täglich
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
Mathematik
Gegen minus unendlich heißt in der Mathematik, dass man für eine Variable, oft das x, in einem Term, zum Beispiel x² gedanklich immer kleinere Zahlen, immer „negativere“ Zahlen einsetzt und zwar, so dass es letztendlich keine kleinste Zahl gibt, die man nicht noch unterschreiten würde. Was dann interessiert ist, was mit dem Wert des Terms passiert. Im Beispiel mit x² würde dieser trotz des ständig kleiner werdenden x-Wertes immer größer werden und selbst gegen plus unendlich streben. Der Grund dafür ist, dass das Quadrat (hoch zwei) aus jeder negativen Zahl wieder eine positive Zahl macht (minus mal minus gibt plus). In einem philosophischen Sinn kann man mit diesem Gedanken zum Beispiel auch nach jedem Zustand des Universums zu einer beliebigen Vergangenheit fragen [1]. Siehe mehr zur mathematischem Idee im Artikel zur mathematischen Idee des => Limes
Mathematik
Gegen plus unendlich heißt in der Mathematik, dass man für eine Variable, oft das x, in einem Term, zum Beispiel 1/x (eins durch x) gedanklich immer größere Zahlen einsetzt und zwar, so dass es letztendlich keine größte Zahl gibt, die man nicht noch überschreiten würde. Was dann interessiert, ist, was mit dem Wert des Terms passiert. Im Beispiel mit 1/x würde dieser mit wachsendem x-Wert ständig kleiner werden: teilt man eins durch eine immer gröeßre Zahl, wird das Ergebnis immer kleiner, es geht gegen Null. In einem philosophischen Sinn kann man mit dieser Denkweise zum Beispiel auch nach dem Endzustand des Universums fragen wenn x für die Zeit steht [1]. Siehe mehr zur mathematischem Idee im Artikel zur mathematischen Idee des => Limes
Mathematik
Für die Funktion f(x)=10:x geht der Funktionswert gegen plus unendlich, wenn x von positiven Werten gesehen gegen 0 geht. Das heißt, wenn man für x immer kleinere Werte wie z. B. 0,1 oder 0,00000001 oder 0,000000000000001 einsetzt, dann wird f(x), also der y-Wert immer größer. Dabei gibt es keine obere Schranke, keine Zahl, die der y-Wert nicht irgendwann einmal überschreiten könnte, wenn man x nur nahe genug an die 0 herangeführt hat. Dieses Denken wird weiter behandelt im Artikel zum mathematischen => Limes
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
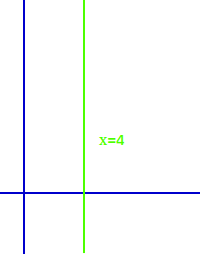Gerade mit unendlicher Steigung
x=4
In einem xy-Koordinatensystem kann eine Gerade senkrecht von unten nach oben eingezeichnet sein. Sie verläuft also parallel zur y-Achse und steht senkrecht auf der x-Achse. Das wird hier kurz besprochen. => Ganzen Artikel lesen …
… Gerade parallel zur y-Achse => Senkrechte Steigung
… ist nicht linear, warum steht unter => senkrechte Gerade
Minus unendlich
-∞
Minus eine Million wäre klein, aber minus eine Milliarde ist noch kleiner, und minus eine Billion ist noch kleiner, aber => Ganzen Artikel lesen …
… geht nicht, mehr dazu unter => Genau Pi
Plus unendlich
… ein unendliche großer Wert, aber auf jeden Fall positiv, siehe z. B. => Grenzwerte über Probieren
… Gerade parallel zur y-Achse => Senkrechte Steigung
… ist nicht linear, warum steht unter => senkrechte Gerade
… eine liegende Acht, siehe unter => Unendlichkeitszeichen
… eine liegende Acht, siehe unter => Unendlichkeitszeichen
Übersicht
Unendlich klein für Zahlen kann heißen, dass die Zahl sehr nahe an der Null ist oder sehr weit links auf der Zahlengeraden. In der Physik wäre dies ein Objekt ohne irgendeine Längenausdehnung. Beide Gedanken sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Mathematik
Minus unendlich oder sehr nahe an der Null: unendlich klein kann in der Mathematik auf zwei unterschiedliche Arten definiert werden. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… gibt einfach nur 0, mehr unter => mal null
… gibt einfach nur 0, mehr unter => mal null
… gibt einfach nur 0, mehr unter => mal null
… gibt einfach nur 0, mehr unter => mal null
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
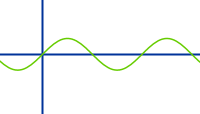Unendliche viele Nullstellen
Beispiele
Als Nullstelle bezeichnet man jeden x-Wert, bei dem der Graph einer Funktion die x-Achse schneidet. Es gibt verschiedene Funktionen, die unendlich viele Nullstellen haben. => Ganzen Artikel lesen …
… heißt in der Mathematik kurz nur => Reihe
… Summen mit einer unendlich großen Anzahl von Summanden (Gliedern), Definition unter => Reihe
