Ganzrationale Funktion
Definition
Die bekanntesten ganzrationalen Funktionen sind die lineare und die quadratische Funktion, z. B. f(x)=4x+8 oder f(x)=x²-8x+15. Daneben gibt es weitere Varianten wie die konstante Funktion wie etwa f(x)=4, die kubische Funktion wie z. B. f(x)=x³ oder die Potenzfunktion. Wesentlich für diese Funktionen ist, dass das x immer nur als Basis einer Potenz vorkommt, das x nur hoch eine natürliche Zahl (oder hoch 0) gerechnet wird und das x niemals im Exponenten einer Potenz oder im Nenner eines Bruches steht. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
Ganzrationale Funktionen
Systematik
Als ganzrational bezeichnet man alle Funktionen, die man in einen gemeinsamen Bauplan umformen kann: (x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + + a₂·x² + a₁·x¹ + a₀. Ganzrationale Funktionen spielen eine herausragende Rolle in der Schulmathematik. Ihre Systematik folgt dem höchsten Exponent (der größten Hochzahl) der Variablen x. => Ganzen Artikel lesen …
… Erklärungen und Aufgaben => Nullstellen von ganzrationalen Funktionen
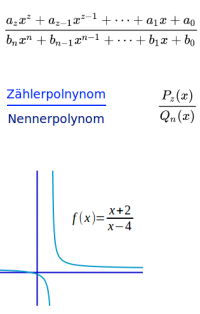Rationale Funktion
Definition
Jede Funktion, die man als Quotient aus zwei ganzrationalen Funktionen schreiben kann nennt man rational. Und nur solche Funktionen gelten als rational. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… Erklärungen und Aufgaben => Nullstellen von ganzrationalen Funktionen
… siehe => Nullstellen von ganzrationalen Funktionen bestimmen
… siehe unter => Ganzrationale Funktionen Diskussion
f(x)= a
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·c·x² + a₁·x¹ + a·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier also 0. Da x⁰ (fast) immer gleich eins ist gilt a·x⁰=a. Man schreibt die Funktion kurz als: f(x) = a⁰. Eine solche Funktion heißt auch => konstante Funktion
f(x) = a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 1. Der Bauplan der Funktion ist also f(x) = a₁·x¹ + a₀·x⁰. Eine solche Funktion heißt auch => lineare Funktion
f(x) = a₂·x² + a₁·x¹ + a₀·x⁰ oder f(x) = ax² + bx + c
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 2. Der Bauplan der Funktion ist also f(x) = a₂·x² + a₁·x¹ + a₀·x⁰. Eine solche Funktion heißt auch => quadratische Funktion
Methoden
f(x)=4x³-3x²+4x-22 wird zu f'(x)=12x²-6x+4: ganzrational nennt man zum Beispiel die linearen, quadratischen und kubischen Funktionen. Hier stehen Regeln und Sonderfälle zum Ableiten einer ganzrationalen Funktion. => Ganzen Artikel lesen …
… f(x) = ax⁸+bx⁷+cx⁶+dx⁵+ex⁴+fx³+gx²+hx¹+i => Grad einer ganzrationalen Funktion
Beispiele
Lineare und quadratische Funktionen sind typische ganzrationale Funktion. Hier steht mit Beispielen kurz erklärt wie man solche Funktionen aufleitet. => Ganzen Artikel lesen …
… siehe unter => Ganzrationale Gleichung aus Versuch
… Tipps und Aufgaben unter => Ganzrationale Funktionen Diskussion
f(x) = a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 3. Der Bauplan der Funktion ist also f(x) = a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰ oder anders geschrieben: f(x) = ax³ + bx³ + cx + d. Eine solche Funktion heißt auch => kubische Funktion
Zum Beispiel f(x) = 10x³-8x²-5x+19 gibt f'(x) = 30x²-16x-5
Eine ganzationale Funktion dritten Grades heißt auch kubische Funktion. Die höchste Potenz von x ist die Zahl 3. Bei der Ableitung entsteht immer eine quadratische Funktion. Die Regeln sind dieselben wie beschrieben unter => ganzrationale Funktion ableiten
f(x) = a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 1. Der Bauplan der Funktion ist also f(x) = a₁·x¹ + a₀·x⁰. Eine solche Funktion heißt auch => lineare Funktion
… f(x) = ax⁵+bx⁴+cx³+dx²+e => quintische Funktion
f(x) = a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 1. Der Bauplan der Funktion ist also f(x) = a₁·x¹ + a₀·x⁰. Eine solche Funktion heißt auch => lineare Funktion
f(x)= a
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·c·x² + a₁·x¹ + a·x⁰ schreiben lässt. Der Grad (oder Rang) gibt an, was die höchste erlaubte Potenz von x ist, hier also 0. Da x⁰ (fast) immer gleich eins ist gilt a·x⁰=a. Man schreibt die Funktion kurz als: f(x) = a⁰. Eine solche Funktion heißt auch => konstante Funktion
f(x) = a₂·x² + a₁·x¹ + a₀·x⁰ oder f(x) = ax² + bx + c
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 2. Der Bauplan der Funktion ist also f(x) = a₂·x² + a₁·x¹ + a₀·x⁰. Eine solche Funktion heißt auch => quadratische Funktion
… Erklärungen und Aufgaben => Nullstellen von ganzrationalen Funktionen
f(x)= a
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·c·x² + a₁·x¹ + a·x⁰ schreiben lässt. Der Grad (oder Rang) gibt an, was die höchste erlaubte Potenz von x ist, hier also 0. Da x⁰ (fast) immer gleich eins ist gilt a·x⁰=a. Man schreibt die Funktion kurz als: f(x) = a⁰. Eine solche Funktion heißt auch => konstante Funktion
… meint dasselbe wie => konstante Funktion
… siehe unter => Ganzrationale Funktionen Steckbriefaufgaben => qck
f(x) = a₄·x⁴ + a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 4. Der Bauplan der Funktion ist also f(x) = a₄·x⁴ + a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰ oder anders geschrieben: f(x) = ax⁴ + bx³ + cx³ + dx + e. Eine solche Funktion heißt auch => quartische Funktion
Zum Beispiel f(x) = 5x⁴+10x³-8x²-5x+19 gibt f'(x) = 20x³+30x²-16x-5
Eine ganzationale Funktion vierten Grades heißt auch quartische Funktion. Die höchste Potenz von x ist die Zahl 4. Bei der Ableitung entsteht immer eine kubische Funktion (hoch drei). Die Regeln sind dieselben wie beschrieben unter => ganzrationale Funktion ableiten
f(x)= a
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·c·x² + a₁·x¹ + a·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier also 0. Da x⁰ (fast) immer gleich eins ist gilt a·x⁰=a. Man schreibt die Funktion kurz als: f(x) = a⁰. Eine solche Funktion heißt auch => konstante Funktion
f(x) = a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 1. Der Bauplan der Funktion ist also f(x) = a₁·x¹ + a₀·x⁰. Eine solche Funktion heißt auch => lineare Funktion
f(x) = a₂·x² + a₁·x¹ + a₀·x⁰ oder f(x) = ax² + bx + c
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 2. Der Bauplan der Funktion ist also f(x) = a₂·x² + a₁·x¹ + a₀·x⁰. Eine solche Funktion heißt auch => quadratische Funktion
f(x) = a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 3. Der Bauplan der Funktion ist also f(x) = a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰ oder anders geschrieben: f(x) = ax³ + bx³ + cx + d. Eine solche Funktion heißt auch => kubische Funktion
f(x) = a₄·x⁴ + a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 4. Der Bauplan der Funktion ist also f(x) = a₄·x⁴ + a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰ oder anders geschrieben: f(x) = ax⁴ + bx³ + cx³ + dx + e. Eine solche Funktion heißt auch => quartische Funktion
f(x) = a₅·x⁵ + a₄·x⁴ + a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰
Eine Funktion heißt ganzrational, wenn sie sich in der Form f(x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + ... + a₂·x² + a₁·x¹ + a₀·x⁰ schreiben lässt. Der Grad gibt an, was die höchste erlaubte Potenz von x ist, hier die 5. Der Bauplan der Funktion ist also f(x) = a₅·x⁵ + a₄·x⁴ + a₃·x³ + a₂·x² + a₁·x¹ + a₀·x⁰ oder anders geschrieben: f(x) = ax⁵ + bx⁴ + cx³ + dx³ + ex + f. Eine solche Funktion heißt auch => quintische Funktion
