Rationale Funktion
Definition
© 2016
- 2026
Basiswissen
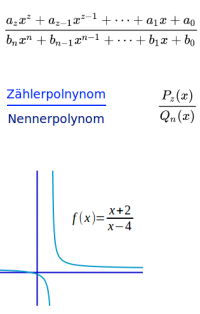
Jede Funktion, die man als Quotient aus zwei ganzrationalen Funktionen schreiben kann nennt man rational. Und nur solche Funktionen gelten als rational. Das ist hier kurz erklärt.
Eigenschaften
- Der Funktionsterm kann als Bruch mit Zähler (oben) und Nenner (unten) geschrieben werden.
- Der Zähler muss sich als ganzrationale Funktion schreiben lassen.
- Der Nenner muss sich als ganzrationale Funktion schreiben lassen.
Arten
Beispiele
- f(x) = 1/x
- f(x) = x/1
- f(x) = x/(x+1)
- f(x) = (x+1)/(x-2)
- f(x) = (4x^2 + 2x + 3)/(x^14 + x^9 - 3)
- Siehe auch 👉 rationale Funktionen