Gebrochenrationale Funktion
Definition
© 2016
- 2025
Basiswissen
Im Zähler und Nenner steht jeweils eine ganzrationale Funktion: der Funktionsterm besteht aus einem Bruch. Sowohl der Zähler als auch de Nenner sind jeweils eine ganzationale Funktion (konstant, linear, quadratisch, kubisch etc.). Das Ganze nennt man dann eine gebrochenrationale Funktion.
Beispiele
- f(x)= [4x³-2x²+4x-5]/[x²+x-1]
- f(x)=(4)/(x+5)
- f(x)=1/x
Definition
- Jede Funktion, deren Term man als P(x)/Q(x) schreiben...
- kann heißt genau dann gebrochenrational, wenn...
- P(x) eine beliebige ganzrationale Funktion ist...
- und Q(x) eine ganzrationale Funktion ist, die ...
- mindestens den Grad 1 hat.
Was darf P(x) sein?
- Das P(x) ist der Funktionsterm im Zähler (oben).
- Es darf irgendeine beliebige ganzrationale Funktion sein.
- Als Zählerterme erlaubt wären zum Beispiel:
- Konstante Funktion, z. B.: 14
- Lineare Funktion, z. B.: 2x+1
- Quadratische Funktion, z. B. 3x²-2x+4
- Kubische Funktion, z. B.: 2x³-x²+4x-5
- Und so weiter mit höheren Graden...
Was darf Q(x) sein?
- Das Q(x) ist der Funktionsterm im Nenner (unten).
- Es darf irgendeine beliebige ganzrationale Funktion...
- sein aber der der Grad muss mindestens 1 sein.
- Konstante Funktionen (nur Zahlen ohne x) sind also verboten.
- Als Zählerterme erlaubt wären zum Beispiel:
- Lineare Funktion, z. B.: 2x+1
- Quadratische Funktion, z. B. 3x²-2x+4
- Kubische Funktion, z. B.: 2x³-x²+4x-5
- Und so weiter mit höheren Graden...
Beispiele
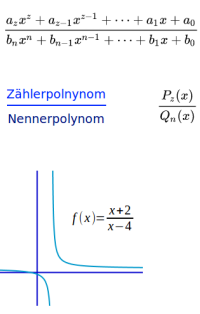
- f(x)=[x+2]/[x-4] ist gebrochenrational.
- Denn: P(x) ist hier x+2. Und das ist ganzrational.
- Und: Q(x) ist hier x-4. Und das ist ganzrational...
- und mindestens vom Grad 1 (also nicht konstant).