Wahrscheinlichkeit
Stochastik
Die Wahrscheinlichkeit ist immer eine Zahl zwischen 0 und 1. [10] Als Wahrscheinlichkeit bezeichnet man den Anteil, auch relative Häufigkeit genannt, eines Ereignisses bei vielen Wiederholungen an der Gesamtzahl der Versuche. Die Wahrscheinlichkeit „ein Sechstel“ beim Würfeln kann zum Beispiel meinen: wenn man sehr oft würfelt, dann kommt meistens in einem Sechstel der Fälle eine 6. => Ganzen Artikel lesen …
Arten
Theoretische, empirische oder bedingte Wahrscheinlichkeit: hier sind verschiedene Arten kurz vorgestellt. => Ganzen Artikel lesen …
Passiert recht sicher
Dass in Deutschland im Sommer die Temperaturen mindestens einmal über 30 °C gehen ist sehr wahrscheinlich. Es passiert so gut wie sicher. Lies mehr zur Mathematik dieser Idee unter => Wahrscheinlichkeit
Stochastik
Die Gegenwahrscheinlichkeit eines Ereignisses ist die Wahrscheinlichkeit dafür, dass das Ereignis nicht eintritt. Die Wahrscheinlichkeit eines Ereignisses plus seine Gegenwahrscheinlichkeit geben in Summe immer genau 1 oder 100. Wenn beim Würfeln die Wahrscheinlichkeit für eine Sechs genau 1/6 ist, dann ist die dazugehörige Gegenwahrscheinlichkeit 5/6. Die Gegenwahrscheinlichkeit ist damit immer auch die Wahrscheinlichkeit für das sogenannte => Gegenereignis
… innerhalb der Stochastik dasselbe wie die => Wahrscheinlichkeitsverteilung
Physik
Ein Feld in der Physik ist eine eindeutige Zuordnung von Eigenschaften für jeden Punkt eines Raumes zu einer bestimmten Zeit. Ordnet man entsprechend eine Wahrscheinlichkeit für ein bestimmtes Ereignis jedem Raum-Zeit-Punkt zu, könnte man in diesem Sinne von einem Wahrscheinlichkeitsfeld sprechen. Obwohl sinngemäß korrekt, ist der Begriff dennoch unüblich und wird nur selten [1] verwendet. => Ganzen Artikel lesen …
Baumdiagramm
Dort wo ein Baumdiagramm endet liegen die Ausgänge. Die Ausgänge sind meistens ganz unten oder ganz rechts in einem Baumdiagramm zu sehen. Die Wahrscheinlichkeiten, die zu jedem einzelnen Ausgang gehören, nennt man entsprechend Ausgangswahrscheinlichkeiten. => Ganzen Artikel lesen …
Bedingte Wahrscheinlichkeit
Definition
Die Wahrscheinlichkeit, dass jemand mit blonden Haaren blaue Augen hat ist höher, als die Warscheinlichkeit, dass jemand mit schwarzen Haaren blaue Augen hat: die Haarfarbe bedingt (beeinflusst) die Wahrscheinlichkeit für Blauäugigkeit. Die Augenfarbe Blau ist damit eine bedingte Wahrscheinlichkeit. Dieser Begriff wird in der Stochastik rechnerisch gefasst und hier kurz erklärt. => Ganzen Artikel lesen …
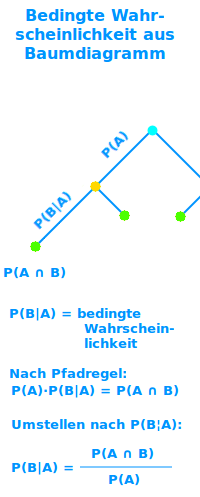Bedingte Wahrscheinlichkeit aus Baumdiagramm
Stochastik
Für zweistufige Zufallsversuche kann man aus einem Baumdiagramm immer bedingte Wahrscheinlichkeiten berechnen. Das ist hier erklärt. => Ganzen Artikel lesen …
Bedingte Wahrscheinlichkeit aus Vierfeldertafel
Stochastik
Aus einer Vierfeldertafel kann man immer bedingte Wahrscheinlichkeiten berechnen. Dabei gibt es 8 Möglichkeiten. Diese sind hier kurz dargestellt. => Ganzen Artikel lesen …
Stochastik
Die Grundformel ist: P(A|B) = P(A∩B)/P(B). Diese Formel ist hier mit Legende kurz vorgestellt. => Ganzen Artikel lesen …
Methoden
Eine bedingte Wahrscheinlichkeit, zum Beispiel geschrieben als P(A|B), kann über Baumdiagramme, Vierfeldtafelen, eine Formel sowie auch über einen Versuch empirisch bestimmt werden. Diese Methoden sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… mit einem Versuch, zum Beispiel => Bedingte Wahrscheinlichkeit über Bayes-Schüssel-Versuch
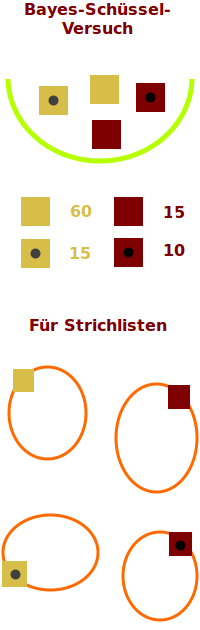Bedingte Wahrscheinlichkeit über Bayes-Schüsselversuch
Empirisch
Bedingte Wahrscheinlichkeiten kann man aus verschiedenen Angaben berechnen oder auch über einen Versuch direkt bestimmten. Hier ist ein beispielhafter Versuch mit einfachem Material vorgestellt. => Ganzen Artikel lesen …
Beispiele
Kopfbehaarung, Titanicopfer, Laktoseintoleranz: diese Phänomene hingen stark von anderen Phänomenen ab und sind damit Beispiele für bedingte Wahrscheinlichkeiten. Diese Beispiele - sowie noch weitere mehr - sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Bornsche Wahrscheinlichkeitsinterpretation
Quantenphysik
In der Quantenphysik werden Naturgesetze nur noch als Wahrscheinlichkeitsaussagen interpretiert: die Wahrscheinlichkeiten geben an, wie oft man im Schnitt ein bestimmtes Messergebnis erhält, wenn ein Versuch sehr oft durchgeführt wird. Betrachtet man die Quantenphysik als letztendlich fundamental, werden alle Naturgesetze zu Wahrscheinlichkeitsgesetzen. Hier ist kurz vorgestellt, was daran so revolutionär sein soll. => Ganzen Artikel lesen …
… in der Stochastik die Wahrscheinlichkeit für ein => Elementarereignis
Empirische Wahrscheinlichkeit
Aus Versuch
Empirische Wahrscheinlichkeit heißt, dass die Wahrscheinlichkeit auf praktische Weise aus einem Versuch oder einer Beobachtung bestimmt wurde. Das Gegenteil einer empirischen Wahrscheinlichkeit ist eine theoretische Wahrscheinlichkeit. Empirisch heißt allgemein so viel wie „aus Erfahrung“ oder „durch Beobachtung“. Rechnerisch ist die empirische Wahrscheinlichkeit eng verbunden mit der relativen Häufigkeit. => Ganzen Artikel lesen …
Stochastik
Ein Ereignis kann sich aus mehreren Ergebnissen (Ausgängen) zusammensetzen. Eine Definition und Beispiele stehen unter => Ereignis
… heißt in der Stochastik oft nur kurz => Ereignis
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
Stochastik
Die Worte Erfolgswahrscheinlichkeit [1] und Trefferwahrscheinlichkeit werden in der Stochastik (Wahrscheinlichkeitsrechnung) mit gleicher Bedeutung, also als Synonyme gebraucht. Hier verwenden wir ds Wort => Trefferwahrscheinlichkeit
… P(A∩B) von A und B => Schnittwahrscheinlichkeit
… im Zusammenhang mit einem Hypotesentest dasselbe wie der => Fehler erster Art
… ein anderes Wort für => bedingte Wahrscheinlichkeit
… gleich große Wahrscheinlichkeiten bei einem Versuch, mehr unter => Laplace-Wahrscheinlichkeiten
… gleich große Wahrscheinlichkeiten bei einem Versuch, mehr unter => Laplace-Wahrscheinlichkeiten
… alle Ergebnisse sind gleich wahrscheinlich, mehr unter => Laplace-Experiment
… gleich große Wahrscheinlichkeiten bei einem Versuch, mehr unter => Laplace-Wahrscheinlichkeiten
… heißt in der Stochastik oft nur kurz => Ereignis
Stochastik
Als objektiv bezeichnet man eine Wahrscheinlichkeit, wenn sie aufgrund von statistisch zuverlässigen Messungen zustande kam [1]. Die objektive Wahrscheinlichkeit ist damit dasselbe wie eine => empirische Wahrscheinlichkeit
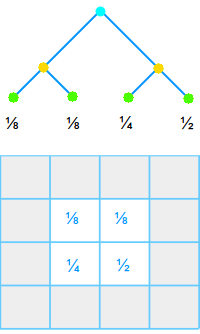Schnittwahrscheinlichkeit
P(A∩B)
P(A∩B) wird gelesen als die Wahrscheinlichkeit von A geschnitten mit B. Sie heißt Schnittwahrscheinlichkeit, Verbundwahrscheinlichkeit oder auch gemeinsame Wahrscheinlichkeit. Sie kommt in Baumdiagrammen und Vierfeldertafeln vor. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Stochastik
Als subjektive Wahrscheinlichkeit bezeichnet man den individuellen Grad an Überzeugung, dass ein Ereignis eintritt oder nicht [1], Grundlage dafür sind oft Vermutungen und innere Überzeugungen [2]. Wenn sich jemand in einem fremden Land vorwiegend an gepflegten touristischen Orten aufhält, kann die Person subjektiv den Eindruck haben, dass die Wahrscheinlichkeit auf arme Menschen zu treffen in dem Land eher niedrig ist. Eine Art Gegenteil ist die sogenannte => objektive Wahrscheinlichkeit
Theoretische Wahrscheinlichkeit
Definition
Man sieht einen normalen, unbeschädigten Spielwürfel: theoretisch müsste die Wahrscheinlichkeit für jede Zahl gleich groß sein, nämlich ein Sechstel. Ob das auch wirklich zutrifft, bleibt ist aber nicht sicher. Das ist hier näher erklärt. => Ganzen Artikel lesen …
