 Wachstum
Wachstum
Mathematisch
Wachstum mathematisch heißt: ein Zahlenwert wird größer. Hier stehen Beispiele, mathematische Arten und Fachworte dazu. => Ganzen Artikel lesen …
 Dachstuhl
Dachstuhl
Das tragende Gerüst, meist aus Holz
Mit dem Begriff Dachstuhl wird in der Regel das gesamte Gefüge eines Dachtragwerks bezeichnet, wenn es als Traggerüst aus einzelnen Traggliedern zusammengesetzt ist und dabei eine traditionelle Dachform ausbildet. Es besteht üblicherweise aus Holz, bei größeren Gebäuden auch aus Traggliedern aus Eisen oder Stahlbeton. Ein gefährliches Tier für einen hölzernen Dachstuhl ist der => Hausbock
 Wachs
Wachs
Kerzenstoff
Wachse sind Stoffe, die bei etwa 40° Celsius schmelzen und dann eine zähflüssige (visose) Flüssigkeit bilden. Chemisch gesehen bestehen Wachse aus langen Kohlenwasserstoffketten. Sie sind unlöslich in Wasser aber gut löslich in z. B. Benzin. => Ganzen Artikel lesen …
 Wachsen
Wachsen
Mathematik | Physik
Eigentlich: größer, länger oder breiter werden. Daneben gibt es noch weitere Bedeutungen (z. B. mit Wachs einreiben). Diese werden hier kurz vorgestellt. Aus Sicht der Mathematik ist das Thema behandelt unter => Wachstum
 Nullwachstum
Nullwachstum
Stagnation
In der Ökonomie auch Stagnation: wichtige volkswirtschaftliche Kenngrößen, etwa das Bruttoinlandsprodukt, wachsen nicht sondern bleiben nahezu konstant. Man spricht von einer => Stagnation
 Haarwachstum
Haarwachstum
Etwa 1 cm/Monat
Menschliche Haare wachsen in einem Monat um etwa 1 Zentimeter bis etwas mehr in die Länge. In einem Jahr können sie bis zu 15 Zentimeter länger werden. Hier folgen einige weitere Fakten zum Haarwachstum bei Menschen. => Ganzen Artikel lesen …
 Baumwachstum
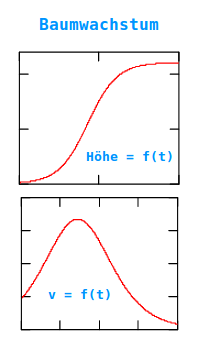
Baumwachstum
Mathematisch
Bäume wachsen mit zunehmendem Alter immer langsamer. Der Graph für die Baumhöhe über der Zeit ist streng monoton wachsend flacht aber nach oben ab. Der Graph für die Wachstumsrate hat oft ein Maximum (schnellstes Wachstum) und geht dann mit zunehmendem Alter gegen den Wert 0. => Ganzen Artikel lesen …
Das was direkt zähl- oder messbar dazukommt
Wenn ein Geldbestand von 800 auf 880 anwächst, dann war der absolute Zuwachs 80 %. Der relative Zuwachs wären 10 % gewesen. Absolut ist das, was in der Einheit dazu kommt, in der man auch die Bestandsmenge angibt. => Ganzen Artikel lesen …
Linear
Man unterscheidet geometrisches und arithmetisches Wachstum. Arithmetisches Wachstum it dabei dasselbe wie ein lineares Wachstum: in gleich großen Zeitabschnitten kommt immer dasselbe dazu. => Ganzen Artikel lesen …
… Liste unter => Wachstumsarten
… Liste unter => Wachstumsarten
 Bash Programme Bevölkerungswachstum
Bash Programme Bevölkerungswachstum
Quellcode
Das Programm simuliert das Wachstum einer Bevölkerung. => Ganzen Artikel lesen …
… Gebirge, Haare, aber auch zur Systematik, siehe unter => Wachstumsarten
… siehe unter => Wachstums- und Abnahmeprozesse
Arten
Beschränkt in der Mathematik heißt: eine gewisse Schranke, also ein bestimmter Zahlenwert wird nicht überschritten oder nicht unterschritten. Es werden drei Arten unterschieden: a) nach oben beschränkt, b) nach unten beschränkt sowie c) nach oben und nach unten beschränkt. Diese sind kurz vorgestellt. => Ganzen Artikel lesen …
 Bevölkerungswachstum
Bevölkerungswachstum
Demographie
Das Wachsen (oder Schrumpfen) der Anzazhl von Individuen in einer Bewölkerung: von etwa 2,5 Milliarden im Jahr 1950 bis auf gut 7,7 Milliarden im Jahr 2020 wuchs die => Weltbevölkerung
 Degressives Wachstum
Degressives Wachstum
Betriebswirtschaftslehre
In der Betriebswirtschaft: wächst immer schwächer, langsamer, weniger => Ganzen Artikel lesen …
 Die Grenzen des Wachstums
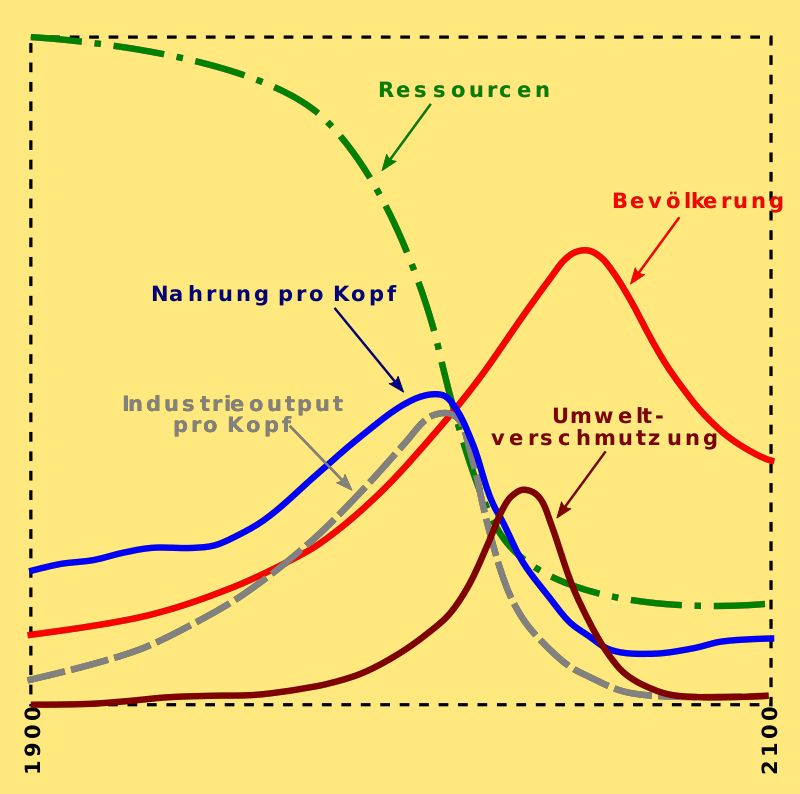
Die Grenzen des Wachstums
Studie
Gegen Mitte des 21ten Jahrhunderts werden viele Bereiche menschlichen Lebens zusammenbrechen: eine auf grenzenloses Wachstum ausgelegte Politik führt zum Kollaps. So in etwa lautet die Kernaussage der Studie mit dem englischen Originaltitel: The Limits to Growth. A Report for the Club of Rome’s Project on the Predicament of Mankind. Die Studie wurde am renommierten Massachussets Institute of Technology erstellt. Die Aussagen basieren auf Computersimulationen. Hier wird noch kurz eine Gegenüberlegung vorgestellt. => Ganzen Artikel lesen …
Besser: Absolutes Wachstum
Angenommen ein Turm wird neu gebaut. Die momentane Höhe sei 100 Meter. Es wird nun ein weiteres Segment (Bauteil) von 5 Metern Höhe oben aufgesetzt. Dann ist der Turm absolut um 5 Meter gewachsen. Relativ zur alten Höhe sind es 5 %. Das direkte Wachstum bezeichnet eher ein => absolutes Wachstum
… Wachstumsfaktor ist konstant, mehr unter => Exponentielles Wachstum
 Exponentielle Wachstumsprozesse
Exponentielle Wachstumsprozesse
Sachbeispiele
Etwas wächst erst langsam und dann immer schneller oder etwas nimmt erst stark und dann immer langsamer ab: beides bezeichnet eine exponentielle Änderung. Mathematisch fasst man beides oft als exponentielles Wachstum zusammen. Hier stehen einige Beispiele zu Sachthemen. => Ganzen Artikel lesen …
… Übersicht unter => Wachstumsmodelle
 Exponentielles Wachstum
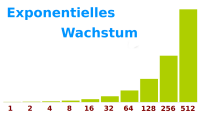
Exponentielles Wachstum
Definition
1 ⭢ 2 ⭢ 4 ⭢ 8 ⭢ 16 ⭢ 32 ⭢ 64 - von einem Schritt zum nächsten Schritt rechnet man immer mit derselben Zahl mal. Hier im Beispiel rechnet man: alter Wert mal zwei gibt den nächsten Wert in der Reihenfolge. Ein solches Wachstum nennt man exponentiell. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Wachstumsfaktor ist konstant, mehr unter => Exponentielles Wachstum
Exponentielles Wachstum
Eine eher unübliche Bezeichnung für ein exponentielles Wachstum: f(x) = a·q^x - der Faktor der die Geschwindigkeit des Wachstums bestimmt ist hier das q. Lies mehr dazu unter => exponentielles Wachstum
… Liste unter => Wachstumsarten
Wachstumsarten
Degressiv, linear, exponentiell, beschränkt oder unbeschränkt: Lies mehr unter => Wachstumsarten
… siehe unter => Freier Fall als proportionales Wachstum
Die Geschwindigkeit wächst linear - und sogar auch proportional - mit der Falldauer. Das proportionale Wachstum ist ein Sonderfall des linearen Wachstums, daher die Weiterleitung zum proportionalen Wachstum.
Fallgeschwindigkeit wächst proportional mit der Falldauer
Von einem Freien Fall spricht man, wenn ein Gegenstand einzig aufgrund der Schwerkraft eines Himmelskörpers nach unten fällt. Vereinfachend geht man dabei normalerweise von einer konstanten Fallbeschleunigung a aus. Für die Erde kürzt man die Fallbeschleunig a oft auch mit g ab. Wir gehen hier auch davon aus, dass zum Beginn des Fallens der Gegenstand keine Geschwindigkeit hatte, also in Ruhe war. Als Faustformel für die Erde gilt: => Ganzen Artikel lesen …
Gefallene Strecke wächst quadratisch mit der Falldauer
Von einem Freien Fall spricht man, wenn ein Gegenstand einzig aufgrund der Schwerkraft eines Himmelskörpers nach unten fällt. Vereinfachend geht man dabei normalerweise von einer konstanten Fallbeschleunigung a aus. Für die Erde kürzt man die Fallbeschleunig a oft auch mit g ab. Wir gehen hier auch davon aus, dass zum Beginn des Fallens der Gegenstand keine Geschwindigkeit hatte, also in Ruhe war. Als Faustformel für die Erde gilt: => Ganzen Artikel lesen …
Definition
Das geometrische Wachstum ist identisch mit dem exponentiellen Wachstum: der Wachstumsfaktor ist über die gesamte Wachstumsphase hinweg konstant, verändert sich also nicht. Geometrisches Wachstum kann mit einer Exponentialfunktion modelliert werden. => Ganzen Artikel lesen …
 Gesetz vom Flächen- und Volumenwachstum
Gesetz vom Flächen- und Volumenwachstum
Kurzbeschreibung
Verdoppelt man alle Längen eines Körpers so, dass seine Form sich dabei nicht verändert, dann hat der Körper danach die Vierfache Oberfläche und das achtfache Volumen. Das hatte bereits Galileo Galilei im Jahr 1638 beschrieben. [1] Dem zugrunde liegt ein tieferes Prinzip, das hier kurz erklärt wird. => Ganzen Artikel lesen …
 Kinderwachstum
Kinderwachstum
Beispielhafte Tabellen
Je jünger Kinder sind desto schneller wachsen sie. Am Anfang sind es noch gut 10 Zentimeter pro Jahr, später, Richtung 20 Jahre Lebensalter ist es nur noch eine Zentimeter in einem Jahr. Hier steht eine Tabelle, unterschieden nach Jungen und Mädchen. => Ganzen Artikel lesen …
Versuch
Man hat einen Klumpen Knete und zerteilt ihn in immer kleinere Stücke. Wie verändert sich dabei die Gesamtoberfläche, also die Fläche, an der die Knete direkt in Kontakt mit Luft steht? Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Wie die Oberfläche bei Zerkleinerung zunimmt
In der Mathematik, Physik oder Chemie: kurze Erklärung von Fachworten, Symbolen und Formeln => Ganzen Artikel lesen …

