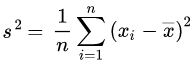Varianz
V oder σ²
Die Varianz ist ein Streuungsmaß aus der Statistik. Der Wert gibt indirekt an, wie weit entfernt Daten einer gemeinsamen Datenliste von ihrem gemeinsamen arithmetischen Mittelwert entfernt sind. => Ganzen Artikel lesen …
… siehe unter => bivariat
Mathematik | Physik
Staucht man eine Parabel entlang der y-Achse, also von oben und unten her, dann bleiben alle Nullpunkte auch nach der Transformation an ihrer alten Stelle: sie sind invariant gegenüber einer Stauchung entlang der y-Achse. Eine Invarianz ist eine Art Immunität gegenüber einer Tätigkeit: eine Eigenschaft, ein Messergebnis, ein Zustand ist invariant gegenüber einer Operation, wenn durch die Operation keine Veränderung bewirkt wird. => Ganzen Artikel lesen …
Kovarianz
Statistik
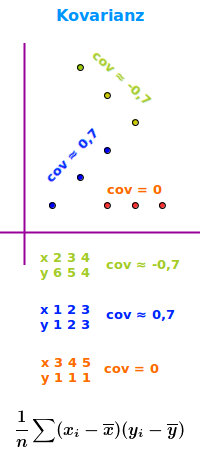
Maß zur Interpretation ob sich zwei Größen in die gleiche Richtung ändern: hat man eine Tabelle mit x-y-Werten oder einen Graphen mit x-y-Punkten, dann kann man die Kovarianz für diese Pärchen von x- und y-Werten ausrechnen. Der Wert der Kovarianz kann von minus unendlich bis plus unendlich gehen. Interpretiert werden kann zunächst nur das Vorzeichen, nicht aber der Betrag (wie weit weg von der Null) des Wertes: => Ganzen Artikel lesen …
Statistik
Die empirische Varianz, ist die Varianz, die tatsächlich durch Beobachtung oder Messung von Daten entstanden ist. Das Gegenteil wäre eine rein theoretische Bestimmung einer Varianz, das wäre nicht empirisch, sondern theoretisch. Zur Varianz an sich siehe unter => Varianz
… für stochastische Prozesse siehe unter => Fixvektor
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
Erklärung mit Zahlenbeispiel
Ausgangspunkt ist immer eine Liste von zusammengehörigen x- und y-Werten. Diese Liste kann als Tabelle geschrieben sein. (Ein Graph mit Punkten sollte man erst in eine Taelle übertragen.) => Ganzen Artikel lesen …
Zahlenbeispiele
Die Kovarianz drückt aus, ob sich der Zusammenhang zweier Größen gut mit je-desto ausdrücken lässt. Hierzu einige knappe Zahlenbeispiele. Die Überschrift gibt die Kovarianz an, darunter steht eine für diese Zahl passende xy-Tabelle. => Ganzen Artikel lesen …
… siehe unter => multivariat
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
Berechnung
Die Varianz und daraus die Wurzel gibt die Standardabweichung. Wenn die Varianz 4,0 ist, dann ist die Standardabweichung 2,0. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
… Erklärung mit Zahlenbeispiel unter => Varianz aus Datenliste
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
… Erklärung mit Zahlenbeispiel unter => Varianz aus Datenliste
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
Physik
Als Translationsinvarianz bezeichnet man die Vorstellung, ein Objekt sich nicht verändert, wenn man es verschiebt oder es von einer anderen Stelle aus betrachtet. Was für Vorgänge im Raum gut vorstellbar ist, trifft aber nicht automatisch auch für Vorgänge in der Zeit zu. [2] => Ganzen Artikel lesen …
… siehe unter => univariat
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
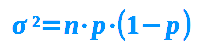Varianz aus Bernoulli-Kette
Formel
σ² = n·p·(1-p) ist die Formel für die Varianz aus der Statistik. Das σ ist das kleine griechische Sigma. Das σ² steht für die sogenannte Varianz, eines von mehreren Streuungsmaßen. Es gibt an, wie weit die Zahlen einer Zahlenliste voneinander entfernt liegen. Das ist hier kurz für Bernoulli-Ketten erklärt. => Ganzen Artikel lesen …
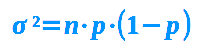Varianz aus Binomialverteilung
V = n·p·(1-p)
Die Varianz ist ein Streuungsmaß und sagt indirekt: wie weit liegen die einzelnen Werte, die in einer Verteilung auftreten, voneinander entfernt. Die Wurzel aus der Varianz ergibt die Standardabweichung. => Ganzen Artikel lesen …
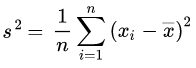Varianz aus Datenliste
Berechnung
Man hat eine Datenliste, also eine Liste von Zahlen, gegeben. Dafür soll die Varianz σ² berechnet werden. Die Varianz ist ein sogenanntes Streuungsmaß. Die Berechnung ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… Erklärung mit Zahlenbeispiel unter => Varianz aus Datenliste
… Erklärung mit Zahlenbeispiel unter => Varianz aus Datenliste
… in der Statistik, siehe unter => Varianz aus Standardabweichung
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
… in der Statistik, siehe unter => Varianz aus Standardabweichung
… Erklärung mit Zahlenbeispiel unter => Varianz aus Standardabweichung
Berechnung
Die Standardabweichung σ hoch zwei gerechnet gibt die Varianz σ² (sigma-quadrat). Ist die Standardabweichung gegeben, kann man daraus sofort die Varianz durch Quadrieren berechnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
