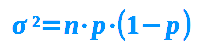Varianz aus Bernoulli-Kette
Formel
© 2016
- 2025
Basiswissen
σ² = n·p·(1-p) ist die Formel für die Varianz aus der Statistik. Das σ ist das kleine griechische Sigma. Das σ² steht für die sogenannte Varianz, eines von mehreren Streuungsmaßen. Es gibt an, wie weit die Zahlen einer Zahlenliste voneinander entfernt liegen. Das ist hier kurz für Bernoulli-Ketten erklärt.
Formel
- σ² = n·p·(1-p)
Legende
- Sigma² = die 👉 Varianz
- Sigma = die 👉 Standardabweichung
- n = die Länge der 👉 Bernoulli-Kette
- p = die Erfolgswahrscheinlichkeit von einem 👉 Bernoulli-Experiment
Rechenbeispiel
- Man würfelt 10 mal.
- Als Erfolg gilt: wenn man eine 6 wirft.
- Das ist eine Bernoulli-Kette aus 10 Bernoulli-Experimenten.
- Die Länge der Bernoulli-Kette n ist also 10.
- Die Erfolgswahrscheinlichkeit p für ein Experiment ist 1/6.
- Die Varianz ist dann 10·(1/6)·(5/6) = 50/36
- Sigma² ist ungefähr 1,4 ✔
Wie kommt man von der Varianz zur Standardabweichung?
- Oft ist die Varianz σ² ein Zwischenschritt zur Berechnung der Standardabweichung.
- Die Standardabweichung ist das σ alleine, ohne Quadrat. Es gibt zwei Rechenwege:
- a) Man berechnet erst die Varianz σ² und zieht daraus dann die Wurzel 👉 Standardabweichung aus Varianz
- b) Man berechnet σ direkt 👉 Standardabweichung aus Bernoulli-Kette