Parameterform der Geraden
Vektorrechnung
x=p+r·u ist die Kurzversion. Sie bedeutet: ein Ortsvektor zu eine beliebigen Punkt auf der Geraden = Stützvektor + r mal Richtungsvektor. Dies ist eine Art, Geraden in einem 2D sowie vor allem auch in einem 3D-Koordinatensystem anzugeben. Die Parameterform der Geraden spielt eine wichtige Rolle in der sogenannten Vektorrechnung (lineare Algebra, analytische Geometrie). Hier wird erklärt, was diese Form einer Geradengleichung anschaulich darstellt. => Ganzen Artikel lesen …
Vektorrechnung
In der Vektorrechnung, auch lineare Algebra oder analytische Geometrie genannt, kann man Geraden und Ebenen mit Hilfe von Parametern und Vektoren angeben. Siehe als Einstieg in das Thema die => Parameterform der Geraden
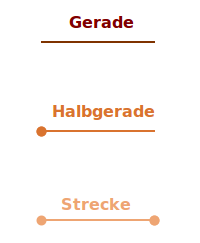Geraden
In der Mathematik: Klassifizierung und Arten
In der Mathematik werden Geraden sowohl innerhalb der Geometrie (2D und 3D) als auch in der Funktionen- und Gleichungslehre behandelt. In der Anylsis spielen sie als Veranschaulichung von linearen Funktionen (Geradengleichung) eine grundlegende Rolle. Es folgen jetzt verschiedene Typen von Geraden. => Ganzen Artikel lesen …
… kann mehrere Dinge bedeuten => Gerade mit Parameter
… mit Stütz- und Richtungsvektor, siehe unter => Parameterform der Geraden
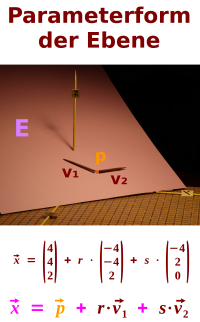Parameterform der Ebene
Vektorrechnung
E: x = p + r mal v1 + s mal v2: p ist der Stützvektor und v1 und v2 sind die zwei Richtungsvektoren: wie diese Gleichung eine Ebene im Raum beschreibt, ist hier kurz erklärt. => Ganzen Artikel lesen …
… kann mehrere Dinge bedeuten => Gerade mit Parameter
Dreidimensional
Hier steht eine Anleitung, wie man ein anschauliches dreidimensionales Bild einer Geraden machen kann, wenn sie in Parameterform gegeben ist. Ein solches Bild im Kopf hilft oft sehr bei der Lösung von Textaufgaben der Vektorrechnung. => Ganzen Artikel lesen …
Anleitung mit Beispiel
Man hat einen Punkt in einem xyz-Koordinatensystem gegeben. Zusätzlich ist noch eine Richtungsangabe bekannt. Daraus soll eine Geradengleichung in Parameterform erstellt werden. Das ist hier erklärt. => Ganzen Artikel lesen …
Anleitung
Zwei Punkte in einem xyz-Koordinatensystem sind gegeben. Daraus soll eine Gleichung mit Stütz- und Richtungsvektor erstellt werden, also eine Geradengleichung in Parameterform. Das ist hier erklärt. => Ganzen Artikel lesen …
… mit Vektoren, siehe unter => Parameterform der Geraden
Anleitung
Man hat eine Geradengleichung in einem xyz-Koordinatensystem in Parameterform gegeben. Parameterform heißt: mit Stütz- und mit Richtungsvektor. Aus dieser Gleichung sollen ein oder mehrere Punkte erzeugt werden. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
