Ausklammern
x ausklammern oder binomische Formel rückwärts denken: das ist hier kurz an Beispielen erklärt. => Ganzen Artikel lesen …
Nullstellen
Beispiele
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
Übersicht
Funktionen wie f(x)=4x+5 oder f(x)=x²-1 werden nach verschiedenen Kriterien klassifiziert. Einige der wichtigsten werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Mathematik
8x+4 kann faktorisiert werden zu 4·(2x+1): faktorisieren heißt so viel wie Ausklammern und dadurch umwandeln in eine Malkette. Die Malkette besteht dann aus einzelnen Faktoren. Daher kommt das Wort. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
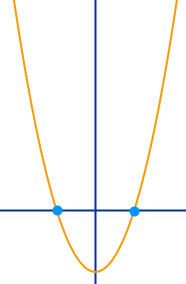Nullstellen von reinquadratischen Funktionen über Faktorisieren
3. binomische Formel rückwärts
0 = 4x²-36 kann mit Hilfe der dritten binomischen Formel gelöst werden. Dieser Weg ist schneller als die Anwendung der pq-Formel (ginge auch). Das ist hier kurz mit einem Beispiel und mit Übungsaufgaben dazu vorgestellt. => Ganzen Artikel lesen …
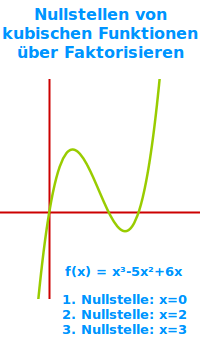Nullstellen von kubischen Funktionen über Faktorisieren
Übersicht
f(x) = x³-x² kann man faktorisieren und erhält dann f(x) = x²·(x¹-1). Für diese umgeformte Variante kann man drei Nullstellen direkt ablesen: 0, -1 und 1. Das Lösungsverfahren ist hier erklärt. => Ganzen Artikel lesen …
… siehe => Nullstellen von kubischen Funktionen bestimmen
