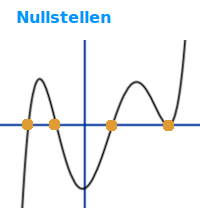
Nullstellen
Beispiele
© 2016
- 2026
Basiswissen|
Konstanten|
Geraden|
Parabeln|
Reinquadratische Funktionen|
Gemischtquadratische Funktionen|
Kubische Funktionen|
Ganzrationale Funktionen|
Hyperbeln|
Exponentialfunktionen|
Trigonometrische Funktionen
Basiswissen
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen.
Konstanten
- f(x)=4 hat keine einzige Nullstelle.
- f(x)=0 hat unendlich viele Nullstellen.
- Mehr unter 👉 Nullstellen von konstanten Funktionen
Geraden
- f(x) = 0 NS bei allen x-Werten
- f(x) = x NS bei 0
- f(x) = 4x + 8 NS bei -2
- f(x) = -0,5x + 1000 NS bei 2000
- Mehr unter 👉 Nullstellen von Geraden
Parabeln
- f(x) = x² NS bei 0
- f(x) = x² -8x + 15 NS bei 3 und 5
- Mehr unter 👉 Nullstellen von Parabeln
Reinquadratische Funktionen
- f(x) = x² NS bei 0
- f(x) = x² - 16 NS bei -4 und 4
- f(x) = 4x² - 100 NS -5 und 5
- f(x) = (x-1)² NS 1
Gemischtquadratische Funktionen
- f(x) = 2x² + 4x - 30 NS 3 und -5
- f(x) = x² + 10x NS 0 und -10
- f(x) = (x+3)·(x-2) NS -3 und 2
Kubische Funktionen
- f(x) = x³ NS 0
- f(x) = x³ - x² NS 0 und 1
- f(x) = (x+1)·(x-2)·(4x-8) NS -1 und 2
- Mehr unter 👉 Nullstellen von kubischen Funktionen
Ganzrationale Funktionen
- f(x) = x NS bei 0
- f(x) = x - 4 NS 4
- f(x) = 2x² - 98 NS 7 und -7
- f(x) = x³ + 2x² - 5x - 6 NS -3; -1 und 2
- f(x) = (x-4)·(x+5)·(x-0,5)·(x+0,3) NS 4; -5; 0,5 und -0,3
- Mehr unter 👉 Nullstellen von ganzrationalen Funktionen
Hyperbeln
- f(x) = 1/x - 4 NS bei 0,25
- f(x) = 4/x - 4 NS bei 1
Exponentialfunktionen
- f(x) = 2^x - 2 NS bei 2
- f(x) = 3^x - 81 NS bei 4
- f(x) = e^(2x-1)-e NS bei 0,5
- Mehr unter 👉 Nullstellen von Exponentialfunktionen
Trigonometrische Funktionen
- f(x) = sin(x) NS bei allen ganzzahligen Vielfachen von 180 Grad
- f(x) = cos(x) NS bei allen ungeradzahligen Vielfachen von 90 Grad
- f(x) = tan(x) NS bei allen ganzzahligen Vielfachen von 180 Grad