 Kreisfläche
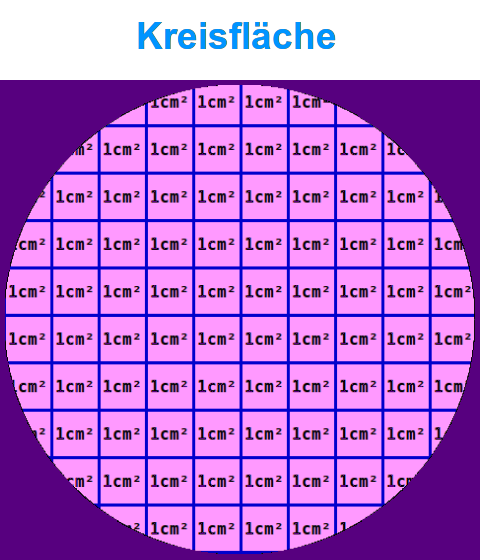
Kreisfläche
⬤ A=πr²
Die Kreisfläche ist die Fläche innerhalb des äußersten Randes eines Kreises. Oft steht Kreifsläche auch kurz für den Inhalt dieser Fläche, etwa in cm². => Ganzen Artikel lesen …
 Kreisflächen
Kreisflächen
Rechenbeispiele
Als Kreisfläche bezeichnet man die Fläche eines Kreises aber auch den Inhalt, oft angegeben in Quadratzentimetern. Dazu stehen hier einige Beispiele => Ganzen Artikel lesen …
… siehe unter => Teilflächen
 Deckfläche
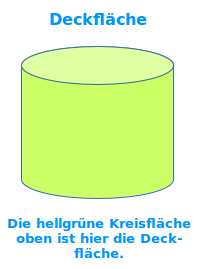
Deckfläche
Geometrie
Bei zum Beispiel einem Zylinder, Prisma oder Quader spricht man oft von einer Deckfläche (oben) und einer Grundfläche (unten). Oft nimmt man an, dass die Grund- und die Deckfläche gleich groß sind. Siehe auch => Grundfläche
 Kreisringfläche
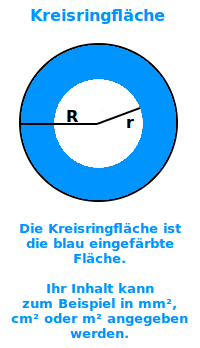
Kreisringfläche
A = π·(R²-r²)
Legende: π ist die Kreiszahl pi (etwa 3,14). Groß R ist der Außen- und klein r ist der Innendurchmesser. Das Ergebnis kann man zum Beispiel angeben in cm² oder m². => Ganzen Artikel lesen …
Gibt es als Wort eigentlich nicht…
Wenn man von Kreisen und ihren Flächen redet, dann meint man immer nur eine Seite von dem Kreis. Das nennt man dann die Kreisfläche. Das Wort Kreisoberfläche gibt es in der offiziellen Mathematik eigentlich nicht. Das Wort Oberfläche bezieht sich in der Mathematik immer auf ausgedehnte (3D) Körper. Siehe auch unter => nicht definiert
… A = pi mal Siehe unter => Kreisfläche berechnen
… A = pi mal Siehe unter => Kreisfläche berechnen
… A = pi mal Siehe unter => Kreisfläche berechnen
… A = pi mal Siehe unter => Kreisfläche berechnen
… A = pi mal Siehe unter => Kreisfläche berechnen
½er Kreis
Man hat einen Kreis und schneidet ihn mit einem geraden Schnitt durch den Mittelpunkt durch. Dadurch entstehen zwei Halbkreise, von der Form her wie ein Halbmond. Wenn man eine dieser halben Kreise nimmt und nur eine Seite davon betrachtet hat man die Halbkreisfläche. Ihr Inhalt ist die Hälfte von der ganzen Kreisfläche. Zur Berechnung siehe auch => Halbkreisfläche berechnen
Formel
½·pi·r·r oder kurz geschrieben als ½·π·r² gibt den Inhalt einer Halbkreisfläche. Das Ergebnis kann man zum Beispiel in Quadratzentimetern (cm²) oder Quadratmetern (m²) angeben. Die Halbkreisfläche ist die Hälfte einer ganzen => Kreisfläche
… A = pi mal Siehe unter => Kreisfläche berechnen
 Kiste 1 Kreisflächenwachstum
Kiste 1 Kreisflächenwachstum
Anleitung
Man zeichnet verschiedene große Kreise. Die Durchmesser sollen immer ganze Zentimeter sein. Dann legt man die Kreisfläche mit 1-cm²-Würfeln aus. Kann man aus dem Durchesser der Kreise die Anzahl der nötigen Würfel vorausberechnen? Wie lautet die Formel? Hier steht eine Schritt-für-Schritt Anleitung für einen Freihandversuch. => Ganzen Artikel lesen …
d = 2·√(A:π)
Kreisfläche durch pi (etwa 3,14) teilen und davon dann die Wurzel ziehen. Das dann noch mal zwei rechnen. Dieses Ergebnis ist dann der Kreisdurchmesser. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… pi mal d² durch 4, mehr unter => Kreisfläche aus Kreisdurchmesser
… pi mal d² durch 4, mehr unter => Kreisfläche aus Kreisdurchmesser
A = π·(D:2)²
Die Kreisfläche, auch Kreisflächeninhalt genannt und zum Beispiel in Quadratzentimetern (cm²) oder Quadratmetern (m²) angegeben, ist gleich der Kreiszahl pi (etwa 3,14) multipliziert mit dem Quadrat des Radiusses. Das ist hier kurz vorgerechnet. => Ganzen Artikel lesen …
 Kreisfläche aus Kreisradius
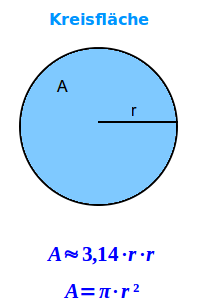
Kreisfläche aus Kreisradius
A = π·r²
Die Kreisfläche, auch Kreisflächeninhalt genannt und zum Beispiel in Quadratzentimetern (cm²) oder Quadratmetern (m²) angegeben, ist gleich der Kreiszahl pi (etwa 3,14) multipliziert mit dem Quadrat des Radiusses. Das ist hier kurz vorgerechnet. => Ganzen Artikel lesen …
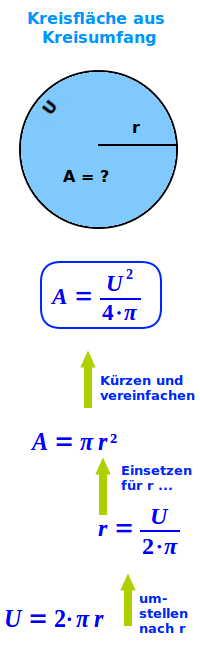 Kreisfläche aus Kreisumfang
Kreisfläche aus Kreisumfang
A = 0,25 mal U² durch pi
A = 0,25 mal U² durch pi: mit dieser Formel kann man aus dem Umfang U eines Kreises direkt den Inhalt A der Kreisfläche berechnen. Die Formel ist hier mit Legende und Herleitung erklärt. => Ganzen Artikel lesen …
… A = pi mal Siehe unter => Kreisfläche aus Kreisradius
… Formel und Herleitung unter => Kreisfläche aus Kreisumfang
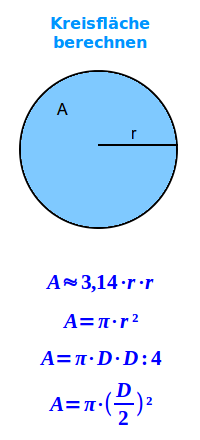 Kreisfläche berechnen
Kreisfläche berechnen
A = π·r²
Pi (etwa 3,14) mal den Radius mit sich selbst malgenommen. Beispiel: für den Radius r = 2 Meter rechnet man: 3,14·2·2 = 12,56 m². Das ist die einfachste Formel. Daneben gibt es noch weitere. Diese werden hier kurz vorgestellt. => Ganzen Artikel lesen …
… zum Beispiel in cm², siehe unter => Kreisfläche
Anleitung
Der Kreisdurchmesser geteilt durch 2 gibt den Kreisradius. Damit weiterrechnen => Kreisfläche aus Kreisradius
Herleitung
Kann man die Formel A = pi·r² aus einfachsten Grundlagen herleiten? Ja, als bekannt angenommen wird nur die Kenntnis darüber, dass der Kreisumfang U immer das Pi-fache des Kreisdurchmessers D ist, also U=Pi·D gilt. => Ganzen Artikel lesen …
… pi mal d² durch 4, mehr unter => Kreisfläche aus Kreisdurchmesser
… A = pi mal => Kreisfläche aus Kreisradius
… U²/(4 mal pi), mehr unter => Kreisfläche aus Kreisumfang
… Formel und Herleitung unter => Kreisfläche aus Kreisumfang
… A = pi mal Siehe unter => Kreisfläche aus Kreisradius
… Formeln unter => Kreisflächenformeln
A = pi mal r²
pi ist immer etwa die Zahl 3,14. Neben dieser Formel gibt es noch verschiedene andere. Einen Einstieg in das Thema bietet die Seite => Kreisfläche berechnen
… A = pi mal Siehe unter => Kreisfläche berechnen

