Extrempunkte
Arten
Extrempunkte sind per Definition nur: Hochpunkte und Tiefpunkte. Hier werden kurz verschiedene Arten (lokal, relative, global, absolut) vorgestellt. => Ganzen Artikel lesen …
Extrempunkt
Definition
Zu den Extrempunkten von Funktionen f(x) zählen nur Hoch- und Tiefpunkte. Man kann Extrempunkte über die erste Ableitung f'(x) und die zweite Ableitung f''(x) bestimmen. Aber mit der schulüblichen Definition der Extrempunkte ergeben sich zwei Probleme, die hier kurz besprochen (und gelöst) werden. => Ganzen Artikel lesen …
Extremwerte
Mathematik
In der Mathematik sind Extremwerte einer Funktion immer nur die y-Werte von Hoch- und Tiefpunkten. Das - und auch weitere Bedeutungen - wird hier kurz vorgestellt. => Ganzen Artikel lesen …
Beispiele
Ein Mittelpunkt ist gleich weit entfernt von den Rändern eines Objektes. Strecken, Kreise oder Kugeln haben zum Beispiel einen Mittelpunkt. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Arten
Nur Hoch- und Tiefpunkte gelten als Extrempunkte. Wendepunkte und Sattelpunkte sind keine Extrempunkte. Lies mehr zur Definition unter => Extrempunkt
… Definition unter => lokaler Extrempunkt
… die höchsten Punkte in einem Intervall => globale Extrempunkte
… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
Extrempunkte berechnen
Methoden
Extrempunkte sind Punkte in einem betrachteten Bereich, zu denen es keine höheren oder keine tieferen Punkte gibt. Um solche Punkte zu berechnen gibt es mehrere Methoden Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
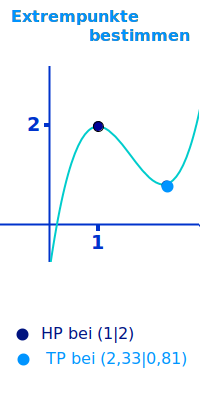Extrempunkte bestimmen
Anleitungen
Zu den Extrempunkten gehören nur Hoch- und Tiefpunkte. Wende- und Sattelpunkte gehören nicht dazu. Hier wird kurz vorgestellt, wie man Hoch- und Tiefpunkte graphisch und rechnerisch bestimmen kann. => Ganzen Artikel lesen …
Anleitung
Ein ausführliches Rechenbeispiel zur Bestimmung eines Extrempunktes von einem Graphen einer Funktion: f(x) = 4² + 16x + 12 => Ganzen Artikel lesen …
… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
… es gibt mehrere => Extrempunkttangenten
Anleitung
Über f'(x); also die erste Ableitung: zu den Extrempunkten eines Funktionsgraphen gehören nur Hoch- und Tiefpunkte. Sind sie Gipfel- oder Talpunkte von einem Graphen, sind sie immer auch lokale Extrempunkte. Hier wird ein Verfahren beschreiben, wie man diese lokalen Extrempunkte rechnerisch über die ersten Ableitung f'(x) und die zweite Ableitung f''(x) bestimmt. => Ganzen Artikel lesen …
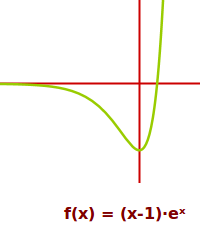Extrempunkte von Exponentialfunktionen
Gibt es nur unter besonderen Bedingungen | Beispiel
Exponentialfunktionen sind Funktionen, bei denen das x im Exponenten einer Potenz vorkommt. Üblicherweise ist die Basis der Potenz eine konstante Zahl, etwa 2 oder auch die eulersche Zahl e. Reine Exponentialfunktionen haben keine Extrempunkte (und auch keine Wendepunkte). Werden sie aber verknüpft mit anderen Funktionen, können Extrempunkte (und auch Wendepunkte) daraus entstehen. Zur Definition siehe auch => Exponentialfunktion
… Es kann keinen, einen oder zwei geben, siehe auch => Kubische Parabel [Graph]
Klärung
Eine konstante Funktion hat als Graphen eine zur x-Achse parallele Linie, also eine waagrechte Linie. Je nach benutzter Definition von Extrempunkt sind entweder alle Punkte dieser Linie Extrempunte oder keiner. Als Extrempunkte bezeichnet man nur Hoch- und Tiefpunkte. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… also Hoch- oder Tiefpunkte, heißen auch => Scheitelpunkt
… Es kann einen, zwei oder drei geben, siehe auch => Quartische Parabel [Graph]
… Hoch- und Tiefpunkte, Definition unter => globaler Extrempunkt
… siehe unter => Extrempunkte bestimmen
Hoch- oder Tiefpunkte von flächenartigen Graphen
Mehrdimensional nennt man Funktionen mit mehr als einer unabhängigen Variablen, zum Beispiel: f(x;y)=x²+y². Der Graph solcher Funktionen kann oft (nicht immer) als Fläche in einem 3D-Koordinatensystem mit x-, y- und z-Achse dargestellt werden. Die Flächen sind oft wellig, gewölbt oder parabelartig. Sie haben oft erkennbare Hoch- und Tiefpunkte. Hoch- und Tiefpunkte fasst man zusammen zu Extrempunkten. Mehrdimensionale Extrempunkte sind also Hoch- oder Tiefpunkte von Funktionen, deren Graph z. B. als Fläche dargestellt werden kann. Anschaulich handhabbar ist das nur für zweidimensionale Funktionen. Lies mehr unter => zweidimensionale Extrempunkte
… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
… die höchsten Punkte in ihrer Nachbarschaft => lokale Extrempunkte
… es gibt mehrere => Extrempunkttangenten
Hoch- und Tiefpunkte
Zweidimensional ist eine Funktion genau dann, wenn sie exakt zwei unabhängige Variablen hat. Ein Beispiel ist die Funktion f(x;y)=x²+y². Ihr Graph wird in einem 3D-Koordinatensystem mit x-, y- und z-Ache dargestellt. Der Graph ist hier eine nach oben geöffnete Schüssel mit dem tiefsten Punkt bei (0|0|0). Dieser Punkt ist also ein zweidimensionaler Tiefpunkt. Analog fasst man auch einen zweidimensionalen Hochpunkt. Lies mehr unter => zweidimensionale Extrempunkte berechnen
Kurzanleitung für f(x;y)
Zweidimensional nennt man Funktionen mit zwei unabhängigen Variablen. Ihre Graphen sind oft Flächen in einem 3D-Koordinatensystem mit x-, y- und z-Achse. Sie zu berechnen heißt, ihre x- und y-Werte zu rechnerisch zu bestimmen. Das Vorgehen ähnelt stark dem eindimensionaler Funktion mit f(x). Das Vorgehen ist hier kurz erläutert. => Ganzen Artikel lesen …
