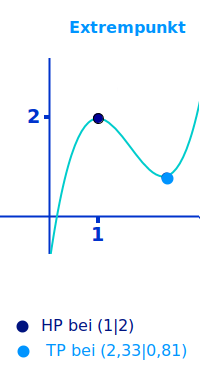
Extrempunkt
Definition
Zu den Extrempunkten von Funktionen f(x) zählen nur Hoch- und Tiefpunkte. Man kann Extrempunkte über die erste Ableitung f'(x) und die zweite Ableitung f''(x) bestimmen. Aber mit der schulüblichen Definition der Extrempunkte ergeben sich zwei Probleme, die hier kurz besprochen (und gelöst) werden. => Ganzen Artikel lesen …
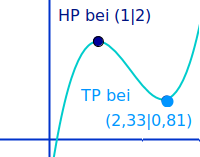Extrempunkte
Arten
Extrempunkte sind per Definition nur: Hochpunkte und Tiefpunkte. Hier werden kurz verschiedene Arten (lokal, relative, global, absolut) vorgestellt. => Ganzen Artikel lesen …
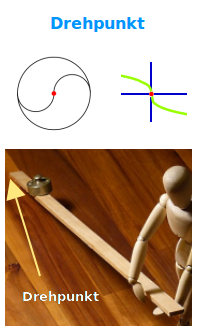Drehpunkt
Geometrie | Graphen | Hebel
Ein Drehpunkt ist ein Punkt, um den anderen Dinge gedreht werden - gedanklich oder tatsächlich. In der Geometrie sowie bei punktsymmetrischen Graphen spricht man allgemein vom Symmetriezentrum. Bei Hebeln (Physik) ist das der Punkt, um den ein Hebel gedreht wird. Die Fälle werden hier kurz erklärt. => Ganzen Artikel lesen …
y-Wert
Als Extremum bezeichnet man den y-Wert von einem Hoch- oder Tiefpunkt. Extremum meint damit dasselbe wie Extremwert. Die Mehrzahl von Extremum ist Extrema. Der x-Wert von Extrema heißt Extremstelle. x und y zusammen heißen Extrempunkt, oft geschrieben als: (Extremstelle|Extremwert). Lies mehr unter => Extremwert
Arten
Nur Hoch- und Tiefpunkte gelten als Extrempunkte. Wendepunkte und Sattelpunkte sind keine Extrempunkte. Lies mehr zur Definition unter => Extrempunkt
Bergbau
Im Bergbau bezeichnet ein Betriebspunkt einen räumlich festgelegten Ort, an dem bergmännische Arbeiten durchgeführt werden: ein Streckenvortrieb, ein Abbau oder eine Kippstelle [1]. Betriebspunkte wurden vor allem zur Zuordnung von anfallenden Kosten definiert, also als => Kostenstelle
… die höchsten Punkte in einem Intervall => globale Extrempunkte
… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
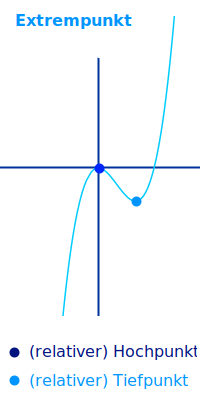Absoluten Extrempunkt berechnen
… über erste Ableitung, siehe unter => globalen Extrempunkt berechnen
… über das Randverhalten, mehr unter => Globalen Extrempunkt berechnen
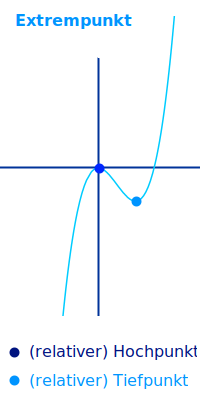Globaler Extrempunkt
… der extremste in einem Intervall, heißt auch => globaler Extrempunkt
… über f' und f'', siehe unter => Extrempunkte berechnen
… mit f'(x) und f''(x) oder auch graphisch => Extrempunkte bestimmen
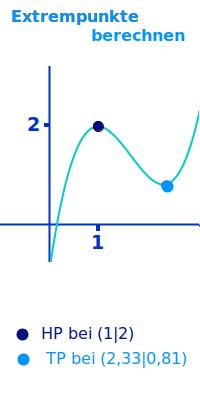Extrempunkte berechnen
Methoden
Extrempunkte sind Punkte in einem betrachteten Bereich, zu denen es keine höheren oder keine tieferen Punkte gibt. Um solche Punkte zu berechnen gibt es mehrere Methoden Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
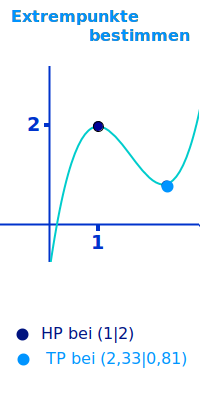Extrempunkte bestimmen
Anleitungen
Zu den Extrempunkten gehören nur Hoch- und Tiefpunkte. Wende- und Sattelpunkte gehören nicht dazu. Hier wird kurz vorgestellt, wie man Hoch- und Tiefpunkte graphisch und rechnerisch bestimmen kann. => Ganzen Artikel lesen …
Anleitung
Ein ausführliches Rechenbeispiel zur Bestimmung eines Extrempunktes von einem Graphen einer Funktion: f(x) = 4² + 16x + 12 => Ganzen Artikel lesen …
… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
… über erste Ableitung und das Randverhalten, mehr unter => Absoluten Extrempunkt bestimmen
… es gibt mehrere => Extrempunkttangenten
Anleitung
Über f'(x); also die erste Ableitung: zu den Extrempunkten eines Funktionsgraphen gehören nur Hoch- und Tiefpunkte. Sind sie Gipfel- oder Talpunkte von einem Graphen, sind sie immer auch lokale Extrempunkte. Hier wird ein Verfahren beschreiben, wie man diese lokalen Extrempunkte rechnerisch über die ersten Ableitung f'(x) und die zweite Ableitung f''(x) bestimmt. => Ganzen Artikel lesen …
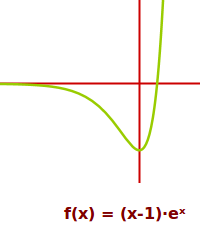Extrempunkte von Exponentialfunktionen
Gibt es nur unter besonderen Bedingungen | Beispiel
Exponentialfunktionen sind Funktionen, bei denen das x im Exponenten einer Potenz vorkommt. Üblicherweise ist die Basis der Potenz eine konstante Zahl, etwa 2 oder auch die eulersche Zahl e. Reine Exponentialfunktionen haben keine Extrempunkte (und auch keine Wendepunkte). Werden sie aber verknüpft mit anderen Funktionen, können Extrempunkte (und auch Wendepunkte) daraus entstehen. Zur Definition siehe auch => Exponentialfunktion
… Es kann keinen, einen oder zwei geben, siehe auch => Kubische Parabel [Graph]
Klärung
Eine konstante Funktion hat als Graphen eine zur x-Achse parallele Linie, also eine waagrechte Linie. Je nach benutzter Definition von Extrempunkt sind entweder alle Punkte dieser Linie Extrempunte oder keiner. Als Extrempunkte bezeichnet man nur Hoch- und Tiefpunkte. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… also Hoch- oder Tiefpunkte, heißen auch => Scheitelpunkt
… Es kann einen, zwei oder drei geben, siehe auch => Quartische Parabel [Graph]
… es gibt mehrere => Extrempunkttangenten
Analysis
Eine Tangente von einem Extrempunkt, also von einen Hoch- oder Tiefpunkt, ist eine Gerade, die genau durch diesen Punkt geht und gleichzeitig die Steigung Null hat, also waagrecht und damit parallel zur x-Achse verläuft. Man unterscheidet zwei Arten. Diese sind hier kurz aufgelistet. => Ganzen Artikel lesen …
… es gibt mehrere => Extrempunkttangenten
… Hoch- und Tiefpunkte, Definition unter => globaler Extrempunkt
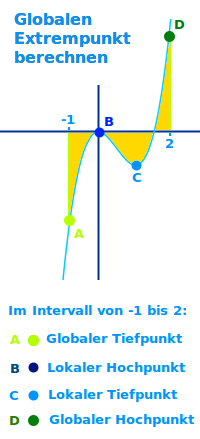Globalen Extrempunkt berechnen
Anleitung
Ein globaler Extrempunkt ist ein Punkt mit dem höchsten oder niedrigsten y-Wert im gesamten Definitionsbereich. Es genügt nicht, nur über die Ableitungen zu suchen. Man muss vielmehr den gesamten Definitionsbereich betrachten. => Ganzen Artikel lesen …
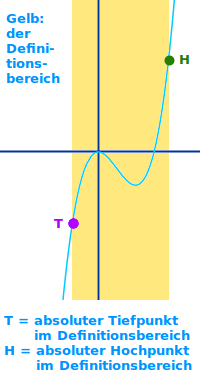Globaler Extrempunkt
Analysis
Es gibt keinen höheren oder tieferen Punkt: ein Punkt auf einem Funktionsgraphen, für den es keinen höheren oder tieferen Punkt sonstwo auf dem Graphen gibt ist ein globaler Extrempunkt. => Ganzen Artikel lesen …
… Definition unter => lokaler Extrempunkt
… siehe unter => Extrempunkte bestimmen
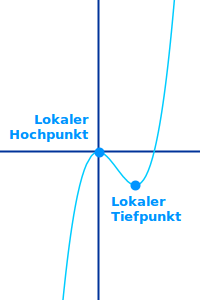Lokaler Extrempunkt
Definition
Zu den Extrempunkten gehören nur Hoch- und Tiefpunkte. Ein lokaler Extrempunkt ist in seiner Umgebung der höchste oder tiefste Punkt. Umgebung meint: beliebig nah links und rechts an diesem Punkt. Anders gesagt: es muss eine Umgebung geben - egal wie klein in der kein Punkt höher oder tiefer ist als dieser Punkt. Siehe auch => Lokale Extrempunkte bestimmen
