Definition

Global

• Global heißt wörtlich übersetzt so viel wie: weltweit, überall
  

• Für Funktionsgraphen heißt es: im gesamten Definitionsbereich.
  

• Der Definitionsbereich sind alle erlaubten x-Werte.
  

• Ist nichts anderes angegeben, meint das: von minus bis plus unendlich.
  

Extrempunkt

• Ein Extrempunkt ist jeder Punkt, der in einer beliebig kleinen Umgebung der höchste oder tiefste Punkt ist.
  

• Das muss aber nicht automatisch der höchste oder tiefste Punkt eines Graphen sein.
  

• Beispiel: der Graph von f(x)=x³-x² hat bei (0|0) einen Hochpunkt.
  

• In seiner Umgebung ist das der höchste Punkt.
  

• Aber schon für x=2 erhält man höherer Punkt, z. B. (2|4).
  

• Ein Extrempunkt muss also nicht der höchste oder tiefste Punkt des ganzen Graphen sein.
  

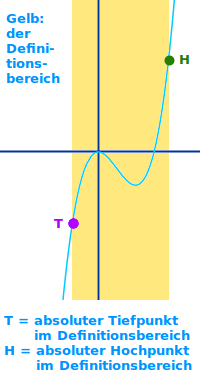
Globaler Extrempunkt

• Ein Punkt, der im gesamten Definitionsbereich extrem ist heißt globaler Extrempunkt.
  

• Ein globaler Extrempunkt ist automatisch immer auch ein lokaler Extrempunkt.
  

• Lokal meint: der Punkt ist auf jeden Fall in seiner näheren Umgebung ein Extrempunkt.
  

• Aber nicht jeder lokale Extrempunkt ist automatisch auch ein globaler Extrempunkt.
  

Bestimmung

• Falls Graph vorhanden, dort ablesen.
  

• Rechnerisch: lokale Extrempunkte über 1. Ableitung bestimmen
  

• Dann: Randverhalten untersuchen
  

• Mehr unter globalen Extrempunkt berechnen ↗