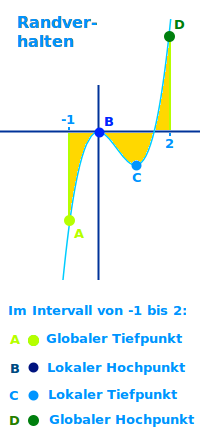
Randverhalten
Kurvendiskussion
© 2016
- 2026
Basiswissen
Rand meint hier die Ränder vom Definitionsbereich einer Funktion, oft am Graphen betrachtet. Das Randverhalten meint dann: Wo liegen die y-Werte einer Funktion, wenn man sehr nah an die Ränder links und rechts vom Definitionsbereich herangeht? Es gibt dann ein Randverhalten links und ein Randverhalten rechts. Das ist hier mit einem Beispiel kurz erklärt.
Definitionsbereich
- Das Wort Randverhalten gehört in das Thema Anylsis (externer Link)
- Es spielt unter anderem eine Rolle bei einer 👉 Kurvendiskussion
- Gegeben ist meist eine Funktion f(x) mit ihrer 👉 Funktionsgleichung
- Gegeben ist meist auch D, der sogenannte 👉 Definitionsbereich
- Definitionsbereich meint hier dasselbe wie 👉 Intervall
- Angenommen D ginge von x=-1 bis x=2.
Randverhalten an einem Beispiel
- Das Randverhalten meint: die y-Werte an den Rändern von D.
- Man unterscheidet einen linken Rand (-1) und einen rechten (2).
- Man bestimmt die y-Werte an den Rändern des Definitionsbereiches.
- Für f(x)=x³-x² wären das zum Beispiel:
- Linker Rand: f(-1) = -2
- Rechter Rand: f(2) = 4
Bedeutung des Randverhaltens
Das Randverhalten spielt eine wichtige Rolle bei sogenannten Extrempunkten. Zu den Extrempunkten gehören nur Hoch- und Tiefpunkte. Sucht man globale (absolute) Extrempunkte in einem Intervall, dann findet man über die Methode mit der ersten Ableitung f'(x) zuverlässig nur sogenannte lokale oder relative Extrempunkte. Das sind sozusagen die Gipfelpunkte von Hügeln oder die die tiefsten Punkte in einem Tal. Es kann aber sein, dass die Funktion an den Rändern des Intervalls noch höhere oder noch tiefere, also extremere y-Werte aufweist. Daher muss man bei der Suche nach globalen (absoluten) Extrempunkten immer überprüfen, ob die y-Werte an einem der Ränder größer (Hochpunkt) oder kleiner (Tiefpunkt) sind als die y-Werte der über f'(x) gefundenen Punkte. Die Rechnung dazu ist näher erklärt auf der Seite 👉 Globalen Extrempunkt berechnen