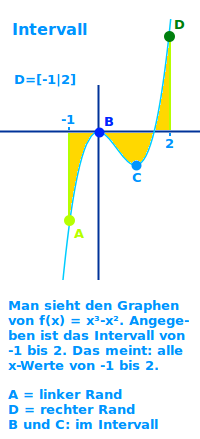
Intervall
Definition
Kurzinfo
Lückenlos aufeinanderfolgende Zahlen nennt man in der Mathematik ein Intervall. Das Intervall von 4 bis 9 meint: alle Zahlen von 4 bis 9, also auch alle Zahlen, die es dazwischen gibt. Die Ränder können, müssen aber nicht dazugehören. Das ist hier kurz vorgestellt.
Ausführliche Definition
Ein Intervall meint: einen zusammenhängenden, lückenlosen Bereich in einer geordneten Trägermenge. Als Trägermenge dient oft der Definitionsbereich. Man betrachtet zum Beispiel die Menge aller natürlichen Zahlen. Die natürlichen Zahlen sind dann der Definitionsbereich oder die Trägermenge. Diese Menge ist geordnet, da man allen Elementen eine klare Reihenfolge geben kann. Ein Intervall ist dann ein Bereich von einem linken (kleinere Zahl) bis zu einem rechten Rand (größere Zahl) bei dem alle Elemente dazwischen lückenlos dazugehören. Siehe auch => Definitionsbereich und Intervall
Beispiele
- Man hat als Trägermenge oder Definitionsbereich: alle natürlichen Zahlen
- Die natürlichen Zahlen sind alle Zählzahlen wie 1, 2, 3, 4, 5 etc.
- Dann bilden die Zahlen 2,3 und 4 zusammen ein erlaubtes Intervall.
- Es gibt keine ausgelassenen Lücken.
Gegenbeispiel
- Man hat als Trägermenge oder Definitionsbereich: alle reellen Zahlen
- Die reellen Zahlen sind alle Zahlen auf dem Zahlenstrahl.
- Zu ihnen gehören insbesondere auch alle "Kommazahlen".
- Hier bilden die Zahlen 2,3 und 4 kein erlaubtes Intervall.
- Die verwendeten Zahlen hängen nicht lückenlos zusammen.
- Zwischen der 2 und 3 gibt es z. B. noch die 2,8.
Die Zugehörigkeit der Ränder
Man unterscheidet, welche der Ränder mit zum Intervall gehören und welche nicht. Die Angabe "vom 12 bis zum 14 Dezember" lässt offen, ob der 12. und der 14. Dezember selbst mit dazugehören oder nicht. Mehr zur Behandlung der Intervallränder unter> Intervalle
Schreibweisen
- Eckige Klammern: nach außen: Rand gehört nicht dazu.
- Eckige Klammern: nach innen: Rand gehört dazu
- Runde Klammern: Rand gehört nie dazu
- Siehe auch => Intervallschreibweisen
