Ebene
Erdkunde, Mathematik
Als Landschaft ist eine Ebene eine große und weitgehend flache Landschaft ohne Hügel, Berge oder Senken. In der Mathematik ist eine Ebene eine Fläche, in die man in jeder Richtung vollständig Geraden hineinlegen kann. => Ganzen Artikel lesen …
Eben
Flach, ohne Berge, Täler
Als eben bezeichnet man meist Landschaften ohne nennenswerte Erhöhungen oder Vertiefungen. Ein Strand ist oft solch eine Ebene Fläche. In der Geographie, Geometrie und vielen anderen Fachgebieten nennt man eine solche Fläche kurz eine => Ebene
Beispiele
Eine Ebene ist sowohl eine flache Landschaft als auch - im mathematischen Sinn - eine unendlich ausgedehnte zweidimensionale Fläche. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Abend
Definition
Laut Duden ist der Abend die Tageszeit um die Abendämmerung, die Zeit des Dunkelwerdens und damit vor der Nacht. Es gibt keine feste Uhrzeit, zu der der Abend beginnt oder endet, der Begriff kann der jeweiligen Situation damit angepasst werden. Eine ganz andere Bedeutunt hingegen hat das Wort => Vorabend
Neben
Ohne etwas anderes dazwischen, direkt als Nachbar
Beispiel: in der Mineraliensammlung lag das gelbe Schwefelstück gleich rechst neben dem dunkelblauen Kupfersulfatkristall. => Ganzen Artikel lesen …
Geometrie
Eine Ebene in der Geometrie ist in sich gesehen immer zweidimensional, kurz also 2D. Das Wort 2D-Ebene wäre also eine Tautologie. Man unterscheidet jedoch flache und gekrümmt Ebenen (beide sind 2d). Die Unterscheidung wird aber erst sinnvoll, wenn man die Ebene in einem 3D-Koordinatensystem betrachtet. Siehe dazu den Artikel => 3D-Ebene
3D-Ebene
Hauptseite
Als 3D-Ebene bezeichnet man Ebenen in einem xyz-Koordinatensystem. Solche Ebenen werden in den Mathematik innerhalb der Vektorrechnung (analytische Geometrie, lineare Algebra) behandelt. => Ganzen Artikel lesen …
… in der Vektorrechnung => Ebenengleichungen
… .. die tatsächlich abgegebene => Nutzleistung
Bei Maschinen spricht man oft von zu- und abgegebener oder zu- und abgeführter Leistung. Sofern in der Maschine keine Energie gespeichert oder aus Speichern abgegeben wird, ist die zugegebene Leistung immer gleich groß wie die abgegebene Leistung. Ein großer Teil der abgegebenen Leistung ist oft aber für den eigentlichen Zweck nutzlos. So geben Verbrennungsmotoren oft bis zu 70 % ihrer Leistung in Form nutzloser Abwärme an. Man hat also als abgegebene Leistung sowowhl die nutzlose Wärmeleistung als auch die gewünschte Bewegungsleistung. Oft meint man mit abgegebener Leistung nur die tatsächlich gewünschte Nutzleistung. Um die Doppeldeutigkeit zu vermeiden, spricht man präzisierend besser von abgegebener => Nutzleistung
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => Abstand von Ebene zu Ebene
Vektorrechnung
Zwei zueinander parallele Ebenen im Raum die nicht identisch sind haben überall denselben Abstand voneinander. Dieser Abstand kann über eine Formel berechnet werden. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Vektorrechnung
Der Abstand einer Ebene zum Koordinatenursprung (0|0|0) in einem 3D-Koordinatensystem ist definiert als die kürzeste Strecke, die von der Ebene zum Punkt (0|0|0) führt. Zur Berechnung eignet sich eine der Normalenformen der Ebene. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… in der Vektorrechnung, siehe unter => Abstand von Punkt zu Ebene
… in der Vektorrechnung => Abstand von Ebene zu Koordinatenursprung
Formel
Verläuft die Gerade nicht parallel zur Ebene, dann haben Gerade und Ebene immer einen Schnittpunkt. In diesem Fall ist der Abstand also immer 0 Längeneinheiten. Verlaufen Gerade und Ebene aber parallel zueinander, dann kann der Abstand berechnet werden. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitungen
Ein Punkt P und eine Ebene E sind gegeben. Der Abstand des Punktes zur Ebene ist die Länge der kürzesten Strecke vom Punkt zur Ebene. Hier stehen Berechnungsformeln. => Ganzen Artikel lesen …
Anleitung
In einem xyz-Koordinatensystem sind ein Punkt (A|B|C) sowie eine Ebene in der hesseschen Normalenform x·n₀ = d gegeben. Eine einfache Formel berechnet den Abstand zwischen Punkt und Ebene. => Ganzen Artikel lesen …
Anleitung
In einem xyz-Koordinatensystem sind ein Punkt (A|B|C) sowie eine Ebene in Koordinatenform gegeben. Daraus kann der Abstand des Punktes von der Ebene leicht berechnet werden. => Ganzen Artikel lesen …
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => Abstand von Ebene zu Ebene
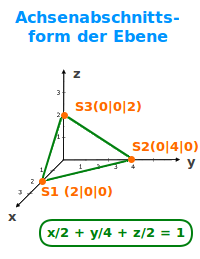Achsenabschnittsform der Ebene
Aufbau
x/xo + y/yo + z/zo = 1: die Zahlen für xo, yo und zo sind die Schnittpunkte mit den 3 Koordinatensachsen. Damit kann man sich die Ebene leicht anschaulich vorstellen. => Ganzen Artikel lesen …
Vektorrechnung
n·x = d ist die allgemeine Normalenform der Ebene. Ausgesprochen heißt das: n skalar multipliziert mit x ergibt für eine gegebene Ebene immer denselben Zahlenwert d. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Astronomie
Die Ebene, in der die Bahn eines Himmelskörpers liegt: von einer Bahnebene spricht man in der Astronomie und verwandten Gebieten. Himmelskörper bewegen sich oft auf Bahnen um einen anderen Himmelskörper, etwa die Erde um die Sonne. Stellt man sich ein flaches Blatt Papier gedanklich so vor, dass die Bahn ganz in dem Papier verläuft, dann ist das Papier die Bahnebene, beziehungsweise ein Teil davon. Die mathematische Ebene wird als unendlich weit ausgedehnt in alle Richtungen gedacht. Siehe mehr zur Definition im Artikel => Ebene
Definition
Bei einer Sammel- oder Zerstreuungslinse werden parallele Strahlen von einer Seite in einem einzigen Punkt auf der anderen Seite zusammengeführt. Dieser Punkt heißt Brennpunkt. Die Brennpunkte aller möglichen Bündel paralleler Strahlen liegen dabei in einer gemeinsamen Ebene, der sogenannten Brennebene. Siehe auch => Brennpunkt
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => Abstand von Ebene zu Ebene
… siehe unter => euklidische Geometrie
- [1] Max Koecher, Aloys Krieg: Ebene Geometrie. Springer Verlag. 2007. ISBN: 978-3-540-49328-0.
… verschiedene Formen Siehe unter => Ebenengleichungen
… also eine Ebene im zweidimensionalen, siehe unter => 2D-Ebene
… also eine Ebene im Raum, siehe unter => 3D-Ebene
